Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 1.10 - Ex. 53
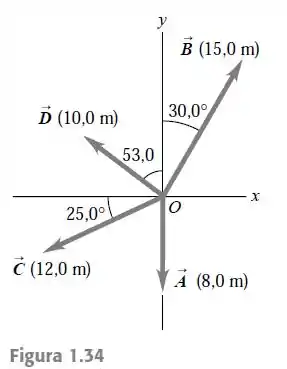
Para os vetores , e indicados na Figura 1.34, ache os produtos escalares a) ; (b) ; (c) .
Passo 1
O “segredo” dessa questão é interpretar os ângulos:
- Sabemos que a o produto escalar resulta em um número, etem uma formulinha, que é dado por:
- Sabemos que a o produto escalar resulta em um número, e é dado por:
- Sabemos que a o produto escalar resulta em um número, e é dado por:
Nós precisamos saber o ângulo que está entre os vetores e :
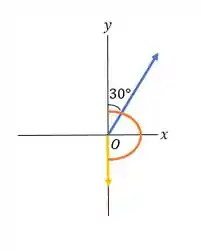
Então fazemos:
E sabemos que :
Agora, vamos substituir os valores:
Passo 2
Nós precisamos saber o ângulo que está entre os vetores e :
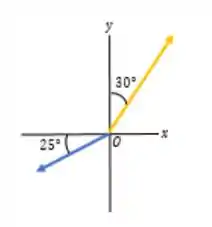
Então fazemos:
E sabemos que :
Agora, vamos substituir os valores:
Passo 3
Nós precisamos saber o ângulo que está entre os vetores e :
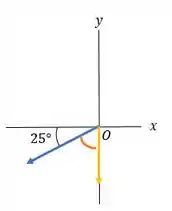
Então fazemos:
E sabemos que :
Agora, vamos substituir os valores:
Resposta
Exercícios de Livros Relacionados
Para os vetores A → e D → indicados na Figura 1.34, a) ache o módulo e a direção do produto vetorial A → × D → ; b) ache o módulo e a direção do produto vetorial D → × A → .
Ache o ângulo entre cada par de vetores:b) A → = 3,0i ^ + 5,0j ^ e B → = 10,0i ^ + 6,0j ^ ;
Por meio de desenhos simples dos produtos vetoriais apropriados, demonstre que A → • B → pode ser interpretado como o produto do módulo de A → vezes o componente de B → em relação a A → , ou o módulo
Ache o ângulo entre cada par de vetores: A → = - 2,0i ^ + 6,0j ^ e B → = 2,0i ^ - 3,0j ^ ;
Qual é o ângulo entre um vetor força F → e o torque τ → gerado por F → ?