Uma surpresa gráfica. No instante , um burrito é lançado a partir de um terreno plano, com uma velocidade inicial de e um ângulo de lançamento . Imagine um vetor posição que ligue o ponto de lançamento ao burrito durante toda a trajetória. Plote o módulo do vetor posição em função do tempo para (a) e (b) . Para , (c) em que instante atinge o valor máximo, (d) qual é esse vlor e a que distância (e) horizontal e (f) vertical está o burrito em relação ao ponto de lançamento? Oara , (g) em que instante atinge o valor máximo, (h) qual é esse valor e a que distância (i) horizontal e (j) vertical está o burrito em relação ao ponto de lançamento?
Passo 1
Queremos encontrar o módulo do vetor em função do tempo. Vamos começar escrevendo esse vetor:
Beleza, então o problema na verdade é escrever as coordenadas e em função do tempo.
Para a coordenada , temos um movimento de velocidade constante, já que não existe nenhuma aceleração agindo na direção horizontal:
E na direção vertical temos que considerar o efeito da aceleação da gravidade:
Podemos substituir isso na expressão que escrevemos para :
Passo 2
E agora podemos calcular o módulo desse vetor:
E podemos arrumar um pouco essa expressão:
E agora podemos fazer os gráficos.
Passo 3
(a) No caso em que , temos:
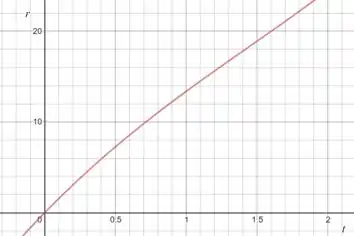
(b) No caso em que :
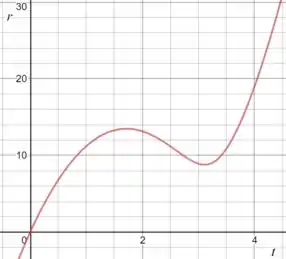
Passo 4
Para encontrar o valor máximo de em função do tempo, precisamos tirar a derivada da nossa função e igualar a zero:
Para derivar a função, vamos deixá-la da seguinte forma:
E então a derivada é:
Como vamos igualar isso tudo a zero, o denominador vai sumir, então:
E garantindo que , podemos dividir tudo por :
Passo 5
(c) No caso em que , essa equação fica da seguinte forma:
Que é uma equação do segundo grau. Mas dê uma olhada no da equação:
Ou seja, temos , portanto não existe solução real para essa equação.
Isso quer dizer que a função não tem ponto de máximo para , e então a distância máxima simplesmente acontece quando o burrito atinge o chão.
Isso quer dizer que temos que calcular o tempo de voo do burrito:
Passo 6
(d) Para calcular o valor de nesse instante nós podemos usar a nossa fórmula:
Passo 7
(e) E a distância horizontal correspondente a essa ponto pode ser calculada usando a fórmula que escrevemos lá em cima para a coordenada :
(f) E como estamos considerando o instante em que o burrito toca o chão, claramente a distância vertical em relação ao ponto de lançamento é zero.
Passo 8
(g) Agora vamos fazer os mesmos cálculos para . Podemos aproveitar a fórmula que escrevemos antes para o ponto de máximo da função :
E podemos resolver essa equação para encontrar :
E daqui tiramos duas raízes: e . Pelo nosso gráfico, podemos ver que o maior deles corresponde a um ponto de mínimo, então a resposta que procuramos é:
Passo 9
(h) O valor de nesse instante pode ser calculado usando a nossa fórmula:
(i) E podemos calcular a distância horizontal usando a fórmula que escrevemos para a coordenada :
(j) E a distância vertical também:
Resposta
(a) Ver gráfico.
(b) Ver gráfico.
(c) .
(d) .
(e) A distância horizontal é de .
(f) A distância vertical é zero.
(g) .
(h) .
(i) A distância horizontal é de .
(j) A distância vertical é de .