Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 26.3 - Ex. 6
A tabela a seguir foi extraída do National Electric Code, que estabelece a corrente máxima considerada segura nos Estados Unidos para fios de cobre isolados de vários diâmetros. Plote a densidade de corrente segura mostrada na tabela em função do diâmetro. Para que calibre de fio a densidade de corrente segura é máxima? ("Calibre" é uma forma de indicar o diâmetro dos fios e 1 mil = 1 milésimo de polegada.)
Passo 1
Olá, meu nobre amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
Aqui temos uma questão que primeiramente lida com conversão de unidades, depois com um plote da densidade de corrente em função do diâmetro.
Então o primeiro passo é expressar a densidade de corrente em unidades do SI convertemos os diâmetros dos fios de mils para polegadas, dividindo por 1000, e depois executamos a conversão de polegadas para metros, multiplicando por 0,0254.
Passo 2
Feito isso, podemos usar a relação
onde A é a área de um círculo
logo
na qual i é a corrente e D é o diâmetro do fio.
Passo 3
Analisando a equação, a densidade de corrente será maior com o menor diâmetro, ao mesmo tempo será maior com o maior corrente.
No caso de um fio calibre 14, por exemplo, e a densidade de corrente segura é
Na verdade, este é o calibre para o qual o valor de J é máximo. O gráfico a seguir mostra a densidade de corrente segura J, em , em função do diâmetro do fio em mils.
Passo 4
Agora basta fazer isto para os valores e traçar o gráfico
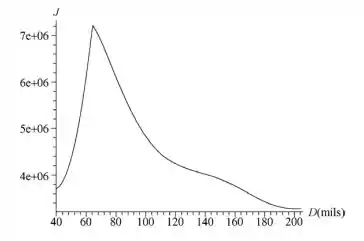
Resposta
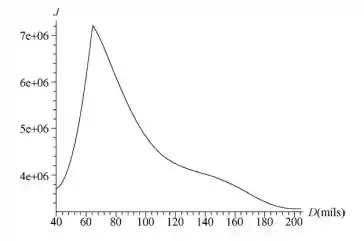64 mils