Um tanque cilíndrico possui um pistão bem ajustado que permite alterar o volume do cilindro. O tanque inicialmente contém 0,110m 3 de ar a uma pressão de 0,355a t m . O pistão é lentamente puxado para fora até que o volume do gás aumenta para 0,390m 3 . Sabendo que a temperatura permaneceu constante, qual é a pressão final?

Enunciado

Física - Young and Freedman - Vol 2- Ed: 14º - Capítulo 18.Exercícios - Ex. 3

Um tanque cilíndrico possui um pistão bem ajustado que permite alterar o volume do cilindro. O tanque inicialmente contém de ar a uma pressão de . O pistão é lentamente puxado para fora até que o volume do gás aumenta para . Sabendo que a temperatura permaneceu constante, qual é a pressão final?

Passo 1

Oii pessoal, show de bola??

“Em tempos de crise, os sábios constroem pontes, enquanto os tolos constroem muros” (T'Challa)”

Bora empurrar e macetar essa questãozinha comigo agora

Para resolver este problema, vamos colocar em prática nosso conhecimento sobre propriedades térmicas da matéria, em que usaremos a equação do gás ideal ao longo de nossa resolução.

A figura abaixo ilustra o nosso problema

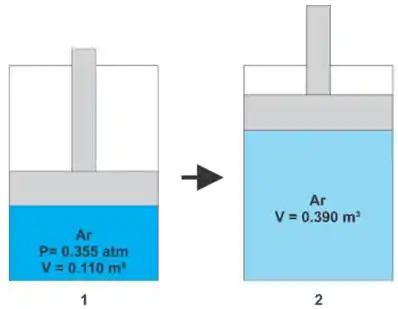
Passo 2

Calcularemos a pressão final no tanque aplicando a equação do gás ideal nos instantes finais e iniciais. Uma vez que o problema afirma que a temperatura permanece constante podemos igualar as duas equações isolando a variável de interesse

"Nós devemos um jeito de cuidar uns dos outros, como se fossemos uma única tribo." (T'Challa)

Resposta

Finalmente temos que a mudança de volume no cilindro a pressão constante causará uma queda na pressão sendo quando .

Exercícios de Livros Relacionados

Em muitos problemas, as propriedades sônicas (*) são valores de referência mais convenientes que as propriedades de estagnação. Para escoamento isentrópico de um gás perfeito, deduza relações para p/p

C O 2 expande isentropicamente, por um duto, de p 1 = 125k P a e T 1 = 100 ° C para p 2 = 80k P a e V 2 = 325m / s . Calcule (a) T 2 , (b) M a 2 , (c) T 0 , (d) p 0 , (e) V 1 e (f) M a 1 .

Mostre que, para escoamento isentrópico de um gás perfeito, se um tubo de Pitot estático mede p 0 ,peT 0 , a velocidade do gás pode ser calculada por V 2 = 2 c p T 0 1 - p p 0 k - 1 k Qual seria uma f

Quando a hipótese de escoamento incompressível começa a falhar para as pressões? Construa um gráfico de p 0 / p para escoamento incompressível de um gás perfeito em comparação com a Equação (9.28a). P

Um gás escoa a V = 200m / s , p = 125k P a e T = 200 ° C . Para (a) ar e (b) hélio, calcule a pressão máxima e a velocidade máxima atingíveis por expansão ou compressão.