Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 14.Exercício - Ex. 39

Um tanque selado que contém água do mar até uma altura igual a 11,0m também contem ar acima da água a uma pressão manométrica igual a 3,0atm. A água escoa para fora através de um pequeno orifício na base do tanque. Calcule a velocidade de efluxo da água.

Passo 1

E aí galera, vamos entender melhor a situação esboçando-a e escolhendo dois pontos:

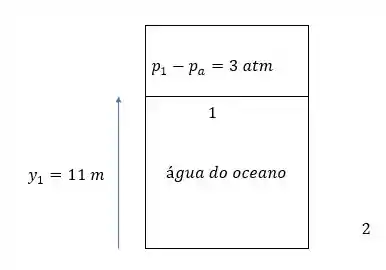
Aplicando a equação de Bernoulli com os pontos 1 e 2 escolhidos como mostrado.

Seja y = 0   no fundo do tanque, então y 1 = 11 m   e y 2 = 0 .

A variável de destino é v 2 .

Passo 2

Temos que

p 1 + ρ g y 1 + 1 2 ρ v 1 2 = p 2 + ρ g y 2 + 1 2 ρ v 2 2

Passo 3

A 1 v 1 = A 2 v 2

Isso implica que

v 1 = A 2 A 1 v 2

Mas a área da seção transversal do tanque ( A 1 )   é muito maior que a seção transversal

área do furo A 2 , então v 1 ≪ v 2 e o 1 2 ρ v 1 2 termo pode ser negligenciado.

Passo 4

Isso nos dá que

1 2 ρ v 2 2 = p 1 - p 2 + ρ g y 1

Usando p 2 = p a e resolvendo para v 2 :

v 2 = 2 ( p 1 - p a ) / ρ + 2 g y 1 = 2 ( 3,039 × 10 5   P a ) 1030   k g / m 3 + 2 ( 9,80   m / s 2 ) ( 11 m )

v 2 = 28,4   m / s

Resposta

v 2 = 28,4   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A entrada da tubulação da figura tem uma seção reta de 0,74m 2 e a velocidade da água é 0,40m / s . Na saída, a uma distância D=180m abaixo da entrada, a seção reta é menor que a da entrada e a veloci
Dois tanques 1 e 2 , ambos com uma grande abertura no alto, contêm líquidos diferentes. Um pequeno furo é feito no lado de cada tanque à mesma distância h abaixo da superfície do líquido, mas o furo d
A água se move com uma velocidade de 5,0m / s em um cano com uma área de seção reta de 4,0c m 2 . A água desce gradualmente 10 m enquanto a seção reta aumenta para 8,0c m 2 . (a) Qual é a velocidade d
O furacão Emily, ocorrido em 1993, apresentava um raio de aproximadamente 350 km. A velocidade do vento ao redor do centro (o "olho") do furacão, de 30 km de raio, atingiu 200 km/h. À medida que o ar
Seu tio está na cabine inferior de seu barco enquanto você está pescando próximo da água. Um arpão errante faz um pequeno furo no casco do barco, e a água começa a escorrer para dentro da cabine. (a)