Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo R.1 - Ex. 34
De acordo com José, o avanço do relógio calculado no Problema é o quanto o relógio está à frente do relógio . Compare este resultado com , onde
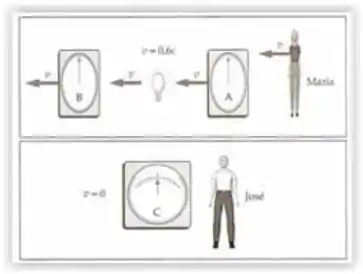
Passo 1
Podemos comparar o tempo calculado no Problema com a equação dada nesta questão avaliando a razão entre ambas
Passo 2
Expressando a razão entre com :
Mas, o valor de é dado por:
Logo, reescrevemos a razão como:
Onde é o tempo encontrado no Problema 33.
Passo 3
Substituindo as variáveis da nossa equação por seus respectivos valores numéricos, chegamos à:
Resposta
A razão entre os tempos é igual a . Logo, o resultado obtido é o mesmo, que para .
Exercícios de Livros Relacionados
13. Em 1975 , um avião transportando um relógio atômico voou para frente e para trás durante 15 horas, em baixa altitude com uma rapidez média de 140m / s , em um experimento de dilatação temporal. O
14. Responda os itens a seguir:(a) Fazendo as suposições necessária e encontrando certas distâncias estelares, estime a rapidez que uma nave espacial teria que ter para levar seus passageiros à estrel
15. Responda os itens a seguir:(a) Compare a energia cinética de um carro em movimento com sua energia em repouso.(b) Compare a energia total de um carro em movimento com sua energia em repouso.(c) Es
17. No referencial de um píon do Problema 16 , qual é a distância percorrida pelo laboratório em 2,6 ∙ 10 - 8s ?
19. No referencial de um múon do Problema 18 , qual a distância percorrida pelo laboratório em 2,2μ s ?