Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo R.1 - Ex. 32
Mostre que o relógio indica quando a luz do atinge o relógio , que se afasta do relógio com rapidez de .
Passo 1
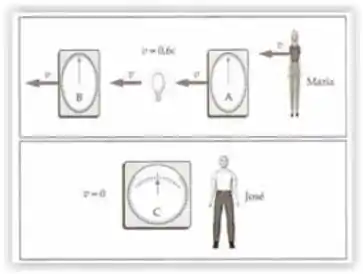
Como a luz do viaja da lâmpada em direção ao relógio com velocidade , o relógio se afasta do relógio com velocidade . A diferença entre essas entre essas distâncias deve ser igual a distância entre o relógio e a lâmpada no instante visto por José.
Passo 2
Expressando a diferença de distâncias viajada pelo de luz e o relógio visto por José como:
Onde é a distância entre os relógios e .
Passo 3
Utilizando a equação de contração de espaço para expressar em termos de :
Substituiremos a equação na e deixaremos isolado:
Passo 4
Trocando as variáveis pelos valores numéricos adequados, chegamos ao nosso resultado:
Resposta
O relógio indica minutos, de fato.
Exercícios de Livros Relacionados
28. A vida média própria de um múon (Veja os problemas 18 e 19 para detalhes sobre os múons) é de 2,20μ s . Considere um múon criado na atmosfera superior da Terra, descendo para a superfície, 8,00k m
29. Um comandante de espaçonave viaja para a Nuvem de Magalhães, com a rapidez uniforme de 0,800 c . Ao sair do cinturão de Kuiper, cuja borda externa está a 50,0U A da Terra (Nota:1U A =150000000k m
Maria é uma funcionária de uma grande plataforma espacial. Ela coloca o relógio A no ponto A e o relógio B no ponto B , distante 100 minutos-luz do ponto A . Ela também coloca uma lâmpada de flash em
36. Uma grande plataforma espacial plana possui, pintado bela, um eixo x . Um rojão explode no eixo x em x 1 = 480m , e um segundo rojão explode no eixo x , 5μ s após, em x 2 = 1200m . No referencial
De acordo com José, o avanço do relógio A calculado no Problema 33 é o quanto o relógio A está à frente do relógio B . Compare este resultado com v L 0 / c 2 , onde v = 0,600c