Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 6.Exercícios e Problemas - Ex. 18
Uma teimosa mula de estanca e se recusa a andar. Para arrastá-la até a estrebaria, o exasperado fazendeiro amarra uma corda na mula e a puxa com o máximo de força que consegue, com de valor. Os coeficientes de atrito entre a mula e o chão são e . O fazendeiro conseguirá arrastar a mula?
Passo 1
Uma dica importante: Em questões que envolvem forças é sempre bom começar fazendo o diagrama de corpo livre, show?
E é isso que vamos fazer primeiro:
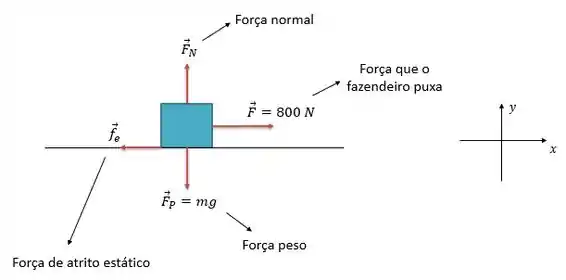
Prontinho! Agora fica bem mais fácil de visualizar as forças que atuam sobre o corpo né? E coloquei ali do ladinho também as direções e que vamos considerar, belezinha?
Outra coisinha também, percebe que ali no diagrama de corpo livre eu coloquei a força de atrito sendo uma força de atrito estático, porque a mula está parada, ela se recusa a andar, então o atrito que age sobre ela é um atrito estático, beleza?
Passo 2
O que a questão nos pergunta é se o fazendeiro irá conseguir mover a mula. Para que ele consiga fazer isso a força com que ele puxa a mula tem que ser maior que a força de atrito estático.
Então bora calcular a força de atrito estático:
O coeficiente foi fornecido pela questão, então precisamos calcular o módulo da força normal.
A mula não se movimenta na direção , então o somatório nas forças na direção tem que ser zero:
A partir disso podemos achar o módulo da força normal:
A questão nos fornece , a massa da mula, e a aceleração da gravidade é conhecida:
Logo:
Passo 3
Agora podemos calcular quanto vale a força de atrito cinético:
O módulo da força de atrito estático é maior que o módulo da força que o fazendeiro puxa a mula, então ele não conseguirá arrastá-la.
Resposta
O fazendeiro não conseguirá arrastar a mula.