Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 6.Exercícios e Problemas - Ex. 23
Uma locomotiva de está deslocando-se a quando falham seu motor e o freio. Que distância percorrerá a locomotiva antes de parar?
Passo 1
Vamos ver as forças que estão atuando sobre a locomotiva:
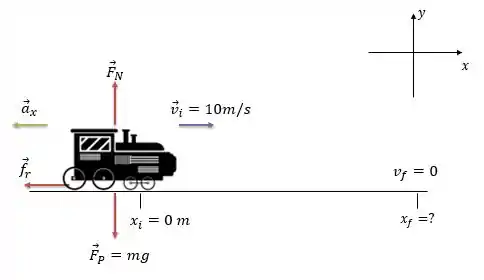
Vamos supor que o freio e o motor da locomotiva falham na posição e nesse momento a locomotiva tem uma velocidade . Como o freio e o motor da locomotiva falharam, a única força na direção que atua é a força de rolamento entre a roda e o trilho, e essa força atua no sentido contrário do movimento.
A velocidade da locomotiva vai diminuindo até que ela atinja , e para isso existe uma aceleração que aponta no sentido contrário ao movimento.
Passo 2
Vamos aplicar a segunda Lei de Newton:
Para esse caso, só existe a força de atrito de rolamento na direção :
Podemos isolar a aceleração:
Passo 3
Para acharmos a aceleração, precisamos achar quem é . Pela fórmula da força de atrito temos:
Para esse caso da locomotiva, onde a roda de aço desliza sobre o trilho que também é de aço, temos que:
Esse valor é encontrado na Tabela 6.1 do livro.
Agora temos que encontrar o valor do módulo da força normal. A locomotiva não se movimenta na direção , então o somatório das forças nessa direção tem que ser zero:
Agora podemos substituir:
Passo 4
Vamos substituir na equação encontrada no passo 2:
o valor de :
A aceleração da gravidade a gente conhece:
Então:
Passo 5
Agora que já encontramos a aceleração, vamos utilizar a equação de Torricelli para encontrar a distância percorrida, :
Temos as seguintes informações:
Vamos substituir e achar :
Resposta
A locomotiva percorrerá .