Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 12.1 - Ex. 71
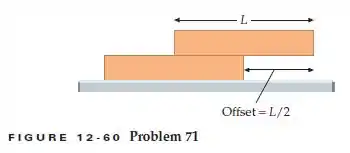
Tem-se um grande número de tijolos idênticos e homogêneos, cada um de comprimento L. Se um for empilhado sobre outro, ao longo de seus comprimentos (veja Figura 12-60), o maior afastamento que permite que o tijolo de cima se equilibre sobre o tijolo de baixo é L/2.
- Mostre que, se esta dupla assim montada for colocada sobre um terceiro tijolo, o afastamento máximo possível do segundo tijolo é L/4.
- Mostre que, em geral, se você tem uma pilha de N tijolos, o afastamento máximo do (n-1)-ésimo tijolo (contando de cima para baixo) sobre o n-ésimo tijolo é L/n.
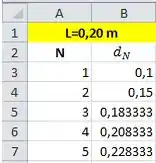
- Escreva um programa para planilha eletrônica que calcule o afastamento total (a soma dos afastamentos individuais) em uma pilha de N tijolos, e determine este valor para L=20cm e N= 5,10 e 100
- A soma dos afastamentos individuais se aproxima de um limite finito, quando Em caso afirmativo, que limite é este?
Passo 1
Beleza galera, olhando assim pode parecer difícil, mas na verdade é bem tranquilo. Vamos pensar sobre esta situação. Nós primeiro vamos colocar estes 2 tijolos sobre um terceiro, e precisamos saber qual será o afastamento existente entre estes dois e o terceiro para manter os três em equilíbrio. E assim por diante até colocar (n-1) tijolos sobre o tijolo de número n. Para que permaneça em equilíbrio este conjunto de tijolos deverá manter um afastamento () do tijolo n.
Vamos ilustrar então:
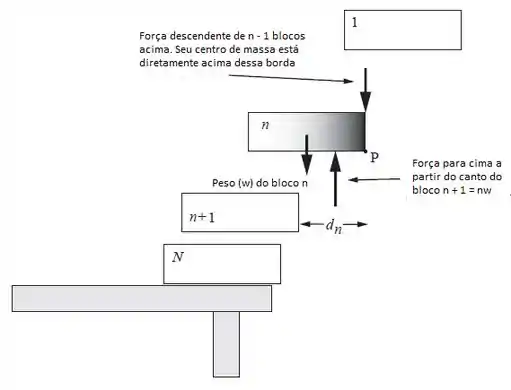
Bom, o sistema está em equilíbrio então temos duas condições para serem satisfeitas:
Vamos começar usando o torque na primeira situação.
O torque é calculado como:
Onde r é a distância entre a força e o eixo de rotação. A escolha do eixo será muito importante, e aqui vamos escolher o ponto P. Neste ponto as forças descendentes resultantes dos blocos acima de n vão passar pelo eixo de rotação e, portanto,
No primeiro bloco, nós vamos ter a força peso (w) sendo aplicada na metade do tijolo (L/2). E depois a força dos n blocos acima de (n+1) irão exercer uma força (nw) no tijolo (n+1) a uma distância .
No torque:
Isolando
Já temos nossa resposta para b, no caso de n tijolos.
Passo 2
Bom, para a letra a temos dois tijolos acima, teremos n=2. Na equação do passo 1:
Para a letra c queremos calcular a distância de n+1, ou seja, vai ser a distância de n tijolos mais a distancia do último
Passo 3
Para finalizar queremos achar o limite do somatório das distâncias:
Devemos lembrar que é uma série harmônica e, por isso, S se aproxima do infinito à medida que o número de blocos N cresce sem limite. Podemos provar plotando o gráfico:
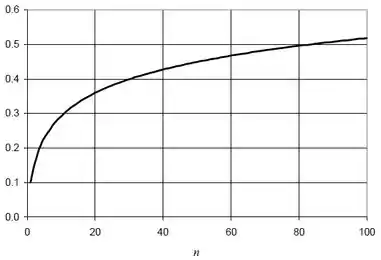
Resposta
- Não existe limite.