Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 16.1 - Ex. 80

Uma onda de pressão harmônica, produzida por uma fonte distante, tem, na região onde você se encontra, frentes de onda planas e vertiais. Faça o sentido + x apontar para o leste e o sentido + y apontar para o norte. A função de onda da onda é p x , y , t = A cos ⁡ ( k x x + k y y - ω t ) . Mostre que o sentido de moviemento da onda forma um ângulo 0 = tan - 1 ⁡ ( k y / k x ) com o sentido + x e que a rapidez da onda é v = ω k x 2 + k y 2   .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Vamos esboçar um diagrama para o sistema. Assim podemos entender melhor o problema:

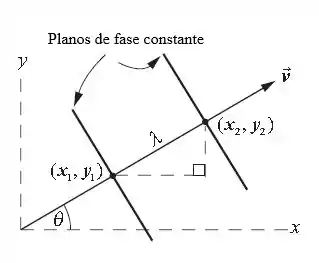
Aplicando o teorema de Pitágoras, temos:

λ = x 2 - x 1 2 + y 2 - y 1 2

λ = ∆ x 2 + ∆ y 2

Sabemos que:

k x = k cos ⁡ θ

k y = k sin ⁡ θ

Portanto, podemos expressar θ como:

θ = tan - 1 ⁡ k y k x

A velocidade da onda é dada por:

v = ω k = ω λ 2 π

Passo 2

A diferença de fase é dada por:

δ = k x x 2 + k y y 2 - ω t - k x x 1 + k y y 1 - ω t

δ = k x ∆ x + k y ∆ y

Como δ = 2 π , temos:

k x ∆ x + k y ∆ y = 2 π

Analisando o diagrama, temos que tan ⁡ θ   também é dada por:

tan ⁡ θ = ∆ y ∆ x

Logo:

∆ y ∆ x = k y k x

∆ y = k y k x ∆ x

Portanto:

k x ∆ x + k y k y k x ∆ x = 2 π

∆ x = 2 π k x k x 2 + k y 2

∆ y = 2 π k y k x 2 + k y 2

Logo:

λ = 2 π k x k x 2 + k y 2 2 + 2 π k y k x 2 + k y 2 2

λ = 2 π k x 2 + k y 2

A velocidade será:

v = ω 2 π 2 π k x 2 + k y 2

v = ω k x 2 + k y 2

Resposta

v = ω k x 2 + k y 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use a equação de onda para determinar a velocidade de uma onda dada em termos de uma função genérica h ( x , t ) : y x , t = 4,00m m h [ 30m - 1 x + 6,0s - 1 t ] .
Uma certa onda transversal senoidal com um comprimento de onda de 20c m está se propagando no sentido positivo ele um eixo x . A Figura mostra a velocidade transversal da partícula situada em x = 0 em
Mostre que a função y = A s e n k x cos ⁡ ω t satisfaz à equação de onda.
Mostre, explicitamente, que as seguintes funções satisfazem à equação da onda ∂ 2 y ∂ x 2 = 1 v 2 ⋅ ∂ 2 y ∂ t 2 :(a) y x , t= k x + v t 3 (b) y x ,t = A e i k x - v t (c) y x ,t = ln ⁡ k x - v t
Dois pulsos de ondas retangulares viajam em sentidos opostos ao longo de uma corda. Em t = 0 , os dois pulsos estão como mostrado na figura. Esboce as funções de onda para t = 1,0 ; 2,0 e 3,0 s .