Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 105

Se um projétil que abandona a arma a 250 m/s deve atingir um alvo 100 m à frente, no memso nível da arma (1,7 m acima do nível do chão), a arma deve apontar para um ponto acima do alvo. (a) A que altura do alvo está este ponto? (b) A que distância, atrás do alvo, o projétil cairá? (Ignore a resistência do ar.)

Passo 1

Oi galera, tudo bem? Vamos tentar visualizar o problema através da figura abaixo:

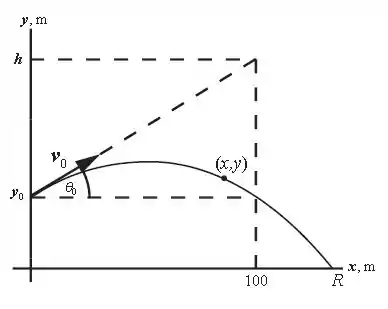
A questão nos pede a altura do alvo em relação ao chão. Ao observarmos o desenho é possível notar que o que queremos achar é o tamanho “h”.

Por este motivo é interessante saber qual o ângulo que a velocidade faz com a horizontal, assim será possível descobrir o valor de h.

x t = x 0 + v 0 x ⋅ t

t = 100 v o x

y t = y 0 + v 0 y ⋅ t - 1 2 ⋅ g ⋅ t 2

0 = 0 + tan ⁡ θ 0 ⋅ 100 - 1 2 ⋅ 9,81 ⋅ 10000 250 2 ⋅ cos 2 ⁡ θ 0

Portanto:

θ 0 = 1 2 sin - 1 ⁡ 100 ⋅ 9,81 250 2

θ 0 = 0,450 °

Com o ângulo podemos fazer uma relação trigonométrica no nosso desenho.

tan ⁡ θ 0 = h 100

h = 100 ⋅ tan ⁡ θ 0

h = 0,7854   m

Passo 2

A questão também nos pede o alcance total da bala. No desenho representado por R.

Para resolver esta parte do problema é só substituir os valores nas equações abaixo.

Portanto:

v x = v 0 x = v o ⋅ cos ⁡ θ 0

v x = 250 ⋅ cos ⁡ 0,45 °

v x = 249,99   m / s  

x t = x 0 + v 0 x ⋅ t

t = R 249,99

y t = y 0 + v 0 y ⋅ t - 1 2 ⋅ g ⋅ t 2

0 = 1,7 + tan ⁡ 0,45 ° ⋅ R - 1 2 ⋅ 9,81 ⋅ R 2 249,99 2

Resolvendo podemos encontrar:

R = 206   m

Porém a pergunta é a que distância atrás do alvo o projétil cairá. Portanto deve-se tirar 100 m para descobrir a distancia entre o alvo e o ponto R.

∆ x = 206 - 100

∆ x = 106   m

Resposta

a )   h = 0,7854   m

b )   ∆ x = 106   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um elétron com uma velocidade horizontal inicial de módulo 1,00 * 10 9c m / s penetra na região entre duas placas de metal horizontais eletricamente carregadas. Nessa região, o elétron percorre uma di
Uma dublê de cinema pula de um helicóptero em vôo a 30 m acima do solo com velocidade constante cujo componente vertical é igual a 10 m / s de baixo para cima e cujo componentehorizontal é igual a 15
Alguns rifles podem disparar uma bala com a velocidade escalar de 965m / s enquanto ela passa pelo cano da arma. Se o cano da arma tem 70,0c m de comprimento e se a bala acelera de forma uniforme dent
O Homem Aranha salta do topo de um edifício alto. Ele cai em queda livre, a partir do repouso até o solo, por uma distância de h. Ele cai uma distância de h/4 no último 1,0 s da sua queda. Qual é a al
Durante os lançamentos, é comum os foguetes descartarem peças desnecessárias. Um certo foguete parte do repouso da plataforma de lançamento e acelera de baixo para cima a constantes 3,30 m / s 2 . Qua