Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 2.5 - Ex. 42
Um tijolo é largado (velocidade inicial nula) do alto de um edifício. Ele atinge o solo em . A resistência do ar pode ser desprezada, de modo que o tijolo está em queda livre.
a) Qual é a altura do edifício?
b) Qual é o módulo da velocidade quando ele atinge o solo?
c) Faça gráficos , e para o movimento do tijolo.
Passo 1
Oi, galerinha! Tudo bom? Temos aqui uma questão de queda livre!
Um tijolo é largado do alto de um prédio e demora pra chegar ao solo. A primeira coisa que queremos saber é a altura do edifício!
Vamos analisar a situação:
Temos um movimento vertical, ou seja, em;
A velocidade inicial é para baixo (já que o tijolo está caindo), então vamos adota-la como ;
O movimento ser na vertical significa que sua aceleração é a gravidade, que é constante e conhecida por nós, ;
Também temos uma queda livre, o que significa que a velocidade inicial é nula, .
Bora lá!
Passo 2
- Para calcularmos a altura do edifício, vamos utilizar a a equação do deslocamento:
Como e o problema nos forneceu que :
Passo 3
b) Para encontrarmos a velocidade com qual o tijolo atinge o solo, vamos utilizar a equação da velocidade:
Passo 4
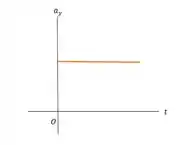
- Agora vamos fazer os gráficos , e para o movimento do tijolo.
No gráfico , temos uma reta horizontal, que representa a aceleração constante:
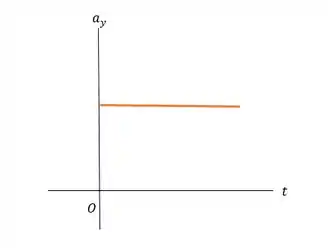
Se a aceleração é constante então o gráfico da velocidade vai ter coeficiente angular constante! Uma vez que a aceleração é a derivada da velocidade em função do tempo. Dessa forma teremos:
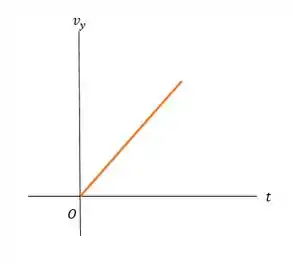
O gráfico da posição vai ter ser de uma função quadrática que passa pela origem. Mas como não existe tempo negativo teremos só metadinha da função quadrática:
Resposta
