Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.3 - Ex. 43

Um engradado grande de massa m está em repouso sobre um piso horizontal. Os coeficientes de atrito entre o piso e o engradado são μ c e μ s . Uma mulher o empurra para baixo exercendo

uma força F → formando um ângulo θ abaixo da horizontal. a) Ache o módulo da força necessária para manter o engradado se movendo com velocidade constante. b) Se μ s for maior do que um valor limite, a mulher não conseguirá mover o engradado por mais força que ela faça. Calcule esse valor crítico de μ s .

Passo 1

Fala aí! como vai?

Vamos analisar o que o enunciado nos diz, esboçar um diagrama de corpo livre.

Como temos uma velocidade, v , constante, isso implica que a aceleração, a , é igual a zero.

A caixa se movendo nos diz que o atrito é cinético, μ c .

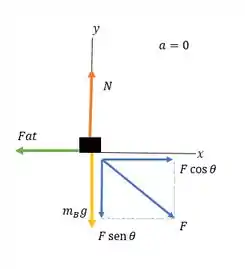
Veja só!

Passo 2

Bom, agora vamos aplicar a 2º Lei de Newton:

  • Para o eixo y :

    • ∑ F y = m ⋅ a y

    N - m ⋅ g - F sen ⁡ θ = 0

    N = m ⋅ g + F sen ⁡ θ

    E

    F a t c = μ c ⋅ N = μ c ⋅ m ⋅ g + μ c ⋅ F sen ⁡ θ

  • Para o eixo x :

∑ F x = m ⋅ a x

F ⋅ cos ⁡ θ - F a t c = 0

F ⋅ cos ⁡ θ - μ c ⋅ m ⋅ g - μ c ⋅ F sen ⁡ θ = 0

F cos ⁡ θ - μ c sen ⁡ θ = μ c ⋅ m ⋅ g

F = μ c ⋅ m ⋅ g cos ⁡ θ - μ c sen ⁡ θ

Tranquilo até aqui?

Passo 3

b) Para a caixa começar a se movimentar, precisamos da mesma força, F , que encontramos no item (a), EXCETO por μ c , este é substituído por μ s :

F = μ s ⋅ m ⋅ g cos ⁡ θ - μ s sen ⁡ θ

Show?

Passo 4

F → ∞ se cos ⁡ θ - μ s sen ⁡ θ = 0 . Isso nos dá que:

μ s = cos ⁡ θ sin ⁡ θ = 1 tan ⁡ θ

Bacana, não é? O que achou? Responde Aí!

Resposta

  1. F = μ c ⋅ m ⋅ g cos ⁡ θ - μ c sen ⁡ θ
  2. F = μ s ⋅ m ⋅ g cos ⁡ θ - μ s sen ⁡ θ , μ s = 1 tan ⁡ θ
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Você precisa empurrar um caixote até um atracadouro. O caixote pesa 165N . O coeficiente de atrito estático entre o caixote e o piso é 0 , 510 e o coeficiente de atrito cinético é 0,32 . A força que v
Uma estudante pretende determinar os coeficientes de atrito estático e atrito cinético entre uma caixa e uma tábua. Para isso, coloca a caixa sobre a tábua e levanta lentamente uma das extremidades da
Diagramas do corpo livre. As duas etapas iniciais para aplicar a segunda lei de Newton para resolver um problema são isolar um corpo para análise e, a seguir, fazer um diagrama do corpo livre para ind
Uma caixa de laranjas de 85N está sendo empurrada ao longo de um piso horizontal. À medida que ela se move, sua velocidade diminui a uma taxa constante de 0,90m / s a cada segundo. A força aplicada po
Uma caixa de massa m é arrastada ao longo de um assoalho horizontal que possui um coeficiente de atrito cinético μ c por uma corda que puxa para cima formando um ângulo θ acima da horizontal com uma f