Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 27.1 - Ex. 84

Passo 1

Escolha o sistema de coordenadas mostrado abaixo. Então a corrente está na direção +z. Suponha que o elétron esteja em ( 1.00 c m , 0 , 0 ) . Podemos usar F = q v xx B para relacionar a força magnética no elétron com v e B e B = (mu_0)/(4 pi) (2 I)/(r) j para expressar o campo magnético na localização do elétron. Vamos precisar expressar v para cada uma das três situações descritas no problema para avaliar F = q v xx B

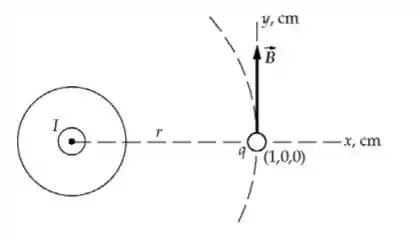
Expresse a força magnética agindo sobre o elétron:

vec F = q vec v xx vec B

Expresse o campo magnético devido à corrente no fio como uma função da distância do fio:

vec B = (mu_0)/(4 pi) (2 I)/(r) hat j

Vamos substituir por B e simplificando temos:

vec F = q vec v xx (mu_0)/(4 pi) (2 I)/(r) hat j = (2 q mu_0 I)/(4 pi r) (vec v xx hat j)

Passo 2

Letra a:

Expresse a velocidade do elétron quando se move diretamente longe do fio:

vec v = v hat i

Substitua por v na equação passada para F e simplifique para obter:

vec F = (2 q mu_0 I)/(4 pi r) ( v hat i xx hat j ) = (2 q mu_0 I v)/(4 pi r) hat k

Substitua os valores numéricos e avalie F:

vec F = (2 (4 pi xx 10^(- 7) N // A^2) (- 1.602 xx 10^(- 19) C) (5.00 xx 10^6 m // s) ( 20.0 A ) hat k)/(4 pi ( 0.0100 m )) = (- 3.20 xx 10^(- 16) N) hat k

F = 3.20 xx 10^(- 16) N e n t r a n d o n a p á g i n a

Passo 3

Letra b:

Expresse v quando o elétron está viajando paralelamente ao fio na direção da corrente:

vec v = v hat k

Substitua na equação de F para obter:

vec F = (2 q mu_0 I)/(4 pi r) (v hat k xx hat j) = - (2 q mu_0 I v)/(4 pi r) hat i

Substitua os valores numéricos e avalie F:

vec F = - (2 (4 pi xx 10^(- 7) N // A^2) (- 1.602 xx 10^(- 19) C) (5.00 xx 10^6 m // s) ( 20.0 A ) hat i)/(4 pi ( 0.0100 m )) = (3.20 xx 10^(- 16) N) hat i

F = 3.20 xx 10^(- 16) N p a r a d i r e i t a

Passo 4

Letra c:

Expresse v quando o elétron estiver viajando perpendicular ao fio e tangente a um círculo ao redor do fio:

vec v = v hat j

Substitua por v na equação de F e simplifique para obter:

vec F = (2 q mu_0 I)/(4 pi r) ( v hat j xx hat j ) = 0

Resposta

  1. F = 3.20 xx 10^(- 16) N e n t r a n d o n a p á g i n a
  2. F = 3.20 xx 10^(- 16) N p a r a d i r e i t a
  3. vec F = (2 q mu_0 I)/(4 pi r) ( v hat j xx hat j ) = 0
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na figura 29-47, parte de um fio longo isolado que conduz uma corrente i = 5,78m A é encurvada para formar uma espira circular de raio R = 1,89c m . Em termos dos vetores unitários, determine o campo
Uma corrente é estabelecida em uma espira constituída por uma semicircunferência de 4,00c m de raio, uma semicircunferência concêntrica de raio menor e dois segmentos retilíneos radiais, todos no mesm
Na figura 29-50, duas espiras circulares concêntricas, que conduzem correntes no mesmo sentido, estão no mesmo plano. A espira 1 tem 1,50c m de raio e conduz uma corrente de 4,00m A . A espira 2 tem 2
Na figura 29-48 mostra, em seção reta, dois fios retilíneos muito longos, ambos percorridos por uma corrente de 4,00A orientada para fora do papel. A distância entre os fios é d 1 = 6,00m e a distânci
Na figura 29-43, o ponto P 2 está a uma distância R = 25,1c m de uma das extremidades de um fio retilíneo de comprimento L = 13,6c m que conduz uma corrente i = 0,693A . (Observe que o fio não é longo