Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 27.1 - Ex. 85

Passo 1

Podemos aplicar a lei de Ampère para derivar expressões para a força do campo magnético em função da distância do centro do fio.

Vamos aplicar a lei de Ampére a um caminho circular de raio r <= R_0 para obtermos:

B_r s R_0 ( 2 pi r ) = mu_0 I_C

Como a corrente é uniforme distribuída ao longo da seção transversal do fio:

(I_C)/(pi r^2) = (I)/(pi R_0^2) => I_C = (r^2)/(R_0^2) I

Substitua por I_C para obter.

B_r <= R_0 ( 2 pi r ) = (mu_0 r^2 I)/(R_0^2)

Resolvendo para B_r <= R_0 temos:

B_r <= R_0 ( 2 pi r ) = (mu_0 r I)/(2 pi R_0^2) = (mu_0)/(4 pi) (2 I)/(R_0^2) r

Passo 2

Vamos aplicar a lei de Ampère a um caminho circular de raio r > R_0 para obter:

B_r > R_0 ( 2 pi r ) = mu_0 I_C = mu_0 I

Resolvendo para B_r > R_0 , temos:

B_r > r = (mu_0)/(4 pi) (2 I)/(r)

Usei o programa de planilha para calcular B em função de r no intervalo 0 <= r <= 10 R_0 . As fórmulas usadas para calcular as quantidades nas colunas são como segue:

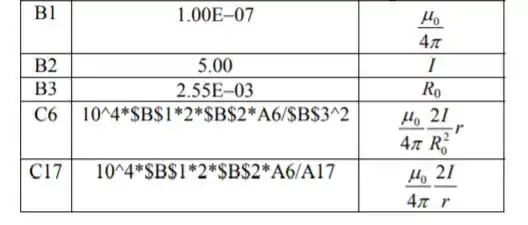
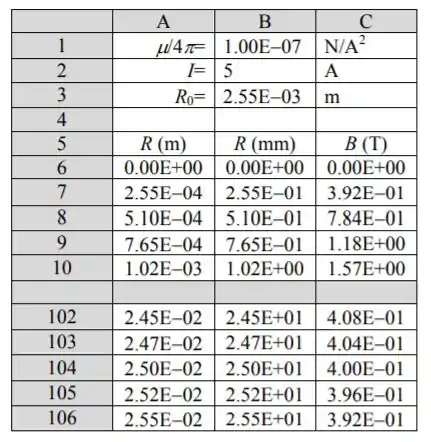
Passo 3

Então, temos um gráfico de B em função de r:

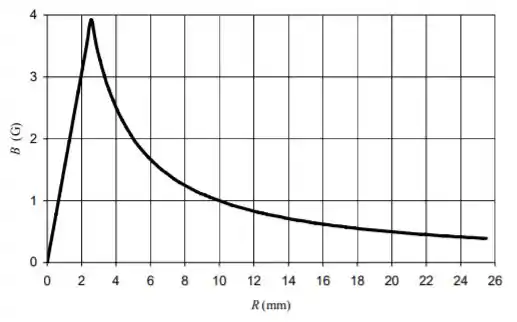
Resposta

Ver gráficos

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

70- O fio indicado na Figura 28.62 possui comprimento infinito e conduz uma corrente I . Determine o módulo, a direção e o sentido do campo magnético resultante produzido pelo fio no ponto P .
66- Os fios que formam as semicircunferências indicadas na figura 28.58 possuem raios a e b . Determine o módulo, a direção e o sentido do campo magnético resultante produzido pelas correntes dos fios
79- Integre B x dado pela Equação ( 28.15 ) , desde - ∞ até + ∞ . Ou seja, faça a integral ∫ - ∞ ∞ B xd x . Explique o significado físico de seu resultado.
68- Um fio circular com diâmetro D repousa sobre uma mesa horizontal e transporta uma corrente I . Na Figura 28.60 , o ponto A marca o centro do círculo e o ponto C está na sua periferia. ( a ) Determ
Um fio muito longo e cilíndrico, de raio R , transporta uma corrente I 0 uniformemente distribuída através da seção reta do fio. Calcule o fluxo magnético através de um retângulo que possui um lado co