O trajeto de um automóvel mostrado na figura abaixo é feito de linhas retas e arcos de círculos. O automóvel parte do repouso no ponto . Depois de chegar até o ponto , ele viaja com rapidez constante até o ponto . Ele retorna ao repouso no ponto . (a) No meio de cada segmento (, , , , e ), qual é a direção do vetor velocidade? (b) Em quais desses pontos o automóvel tem uma aceleração diferente de zero? (c) Como se comparam as magnitudes das acelerações para os segmentos e ?
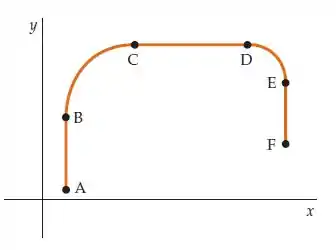
Passo 1
(a) O vetor da velocidade vai apontar na direção da variação do vetor posição. Podemos representar isso no desenho da seguinte forma:
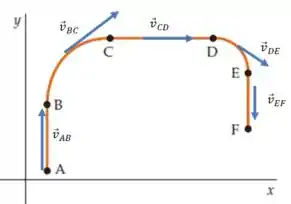
Aqui estamos preocupados apenas com as direções dos vetores, então a magnitude está completamente fora de escala.
Passo 2
(b) Para que a aceleração seja diferente de zero a velocidade deve estar mudando de alguma forma, seja em magnitude, sentido ou direção.
Segundo o enunciado, a rapidez aumenta entre os pontos e , então a aceleração é diferente de zero nesse trecho.
Entre os pontos e a rapidez é constante, então só teremos aceleração nos trechos que não são retos, pois nesses casos a direção está mudando. Isso vale para e .
Como a rapidez reduz entre os pontos e , também temos aceleração nesse trecho.
Portanto a aceleração é diferente de zero em todos os trechos exceto .
Passo 3
(c) Agora queremos compara as acelerações nos trechos e .
Em ambos os trechos a rapidez é constante, e a única aceleração que existe é a centrípeta, associada à trajetória circular nesses trechos. A magnitude da aceleração centrípeta segue a seguinte fórmula:
Como é igual nos dois trechos, a única diferença está no raio de curvatura, que é maior para o trecho , e portanto a sua aceleração é menor:
Resposta
(a) Ver desenho.
(b) Diferente de zero para todos os trechos exceto .
(c) A aceleração tem magnitude maior em .