Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 10.Exercícios e Problemas - Ex. 76
Um trenó parte do repouso do topo da colina hemisférica, coberta de neve e livre de atrito, mostrada na figura a seguir.
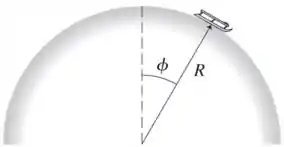
- Obtenha uma expressão para o módulo da velocidade do trenó quando sua posição angular é dada pelo ângulo .
- Use as leis de Newton para determinar a máxima velocidade que o trenó pode ter, para um dado valor de , sem perder contato com a superfície.
- Para que ângulo o trenó “decola” da superfície?
Passo 1
Se liga! Vamos resolver o item (a).
No topo da colina o trenó está em repouso, ou seja, . Sendo assim, só tem energia potencial gravitacional. Pela conservação da energia, temos que
A altura inicial é . Sendo assim
A altura final é . Portanto
A energia cinética é dada por
Retornando para equação da conservação da energia mecânica, temos
Isolando a velocidade temos
Passo 2
Agora vamos resolver o item (b).
Para que o trenó se mantenha na trajetória semicircular é necessário que exista uma resultante centrípeta. Vamos descrever as forças. Se liga na figura.
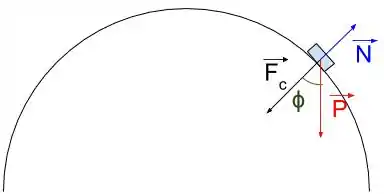
A componente do peso na direção radial é dada por
Aplicando a 2ª Lei de Newton temos
Para que o trenó pare de tocar a colina e necessário que
Sendo assim, temos
Passo 3
No item (c) queremos saber para que valor de o trenó sai da superfície da colina. Para saber onde isso acontece, basta igualarmos as velocidades encontradas nos itens (a) e (b).
Elevando os dois lados ao quadrado, temos
Agora podemos aplicar o arco-cosseno para achar o valor de .