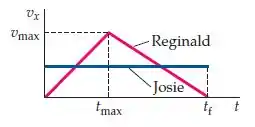
Reginaldo saiu para uma corrida matinal, e durante o seu exercício em uma pista reta ele tem uma velocidade que depende do tempo conforme mostrado na figura. Ou seja, ele parte do repouso, e termina em repouso, atingindo um pico de velocidade v m á x á em um tempo arbitrário t m á x á . Uma segunda corredora, Josie, corre pelo intervalo de tempo de t = 0 até t = t f à velocidade constante v J , de forma que cada um dos dois tem o mesmo deslocamento durante o intervalo. Nota: t f não é o dobro de t m á x á , mas representa um tempo arbitrário. Qual é a relação entre v J e v m á x á ?

A relação é v J = 1 2 v m a x .

Enunciado

A informação mais importante aqui é o fato de que o deslocamento total durante o intervalo é igual para os dois.

O que é o deslocamento em um gráfico de velocidade em função do tempo? É a área sob o gráfico.

Começamos calculando a área sob o gráfico da velocidade do Reginaldo, que tem o formato de um triângulo:

Agora vamos calcular a área sob o gráfico da velocidade da Josie, que é um retângulo:

Lembrando que os dois deslocamentos são iguais:

E então a relação entre as velocidades é:

A relação é .