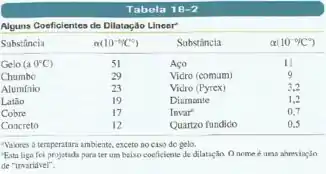
Três barras retilíneas de mesmo comprimento, feitas de alumínio, Invar e aço, todas a , formam um triângulo equilátero com pinos articulados nos vértices. A que temperatura o ângulo oposto à barra de Invar é ? As fórmulas trigonométricas necessárias estão no apêndice E e os dados necessários estão na Tabela .
Passo 1
Ok, vamos começar desenhando a situação:
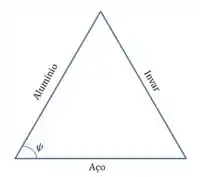
O enunciado diz que, no começo, o triângulo é equilátero. Então tá, o que isso quer dizer? Primeiro, claro, que todos os lados são iguais, e segundo que todos os ângulos também são, e medem:
Agora nós vamos aquecer esse triângulo, e a pergunta é a seguinte: o quanto a gente tem que aquecer pra que o ângulo oposto à barra de Invar (que está marcado ali na figura como ), meça ?
Passo 2
Bom, conforme a temperatura vai aumentando, a gente sabe que o comprimento de cada lado aumenta por essa fórmula aqui:
O de cada material foi dado naquela tabela. Agora vem a questão? Como a gente pode relacionar o comprimento dos lados com aquele ângulo que a gente quer “controlar”?
Vamos usar a lei dos cossenos!
Beleza, agora vamos substituir aquela fórmula da dilatação (pra cada um dos materiais) nessa equação.
Passo 3
Lembre sempre que, como o triângulo começa equilátero, o é o mesmo pra todos.
Muita coisa né? Mas vamos arrumar um pouco. Primeiro podemos cortar o , que aparece em todos os termos:
Agora vamos pensar o seguinte, quando a gente elevar esses parênteses aí ao quadrado, vai ficar mais ou menos assim:
Mas pensa bem: os coeficientes de dilatação já são aí da ordem do , concorda? E a variação de temperatura também vai ser bem pequena, já que só queremos mudar o ângulo de pra . Quando a gente elevar essas coisas muito pequenas ao quadrado, elas vão ficar ainda mais insignificantes!
Então o que a gente vai fazer (e isso é muito comum na física) é ignorar esses termos que vão ficar ao quadrado, porque eles não vão fazer nenhuma diferença na nossa questão.
Passo 4
Ok, agora sim, vamos abrir os parênteses (já ignorando os termos que tem
Vamos continuar arrumando:
Agora vamos tentar isolar :
Vamos dividir em cima e embaixo por dois:
Ótimo, agora é só substituir os valores:
Ok, essa é a variação de temperatura. Então a temperatura final é:
E então:
Ótimo! Deu trabalho, mas conseguimos.
Resposta
Esse ângulo ocorre quando