Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 16

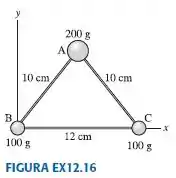
As três massas mostradas na FIGURAEX12.16 estão ligadas por hastes rígidas e de massas desprezíveis.

a. Determine as coordenadas do centro de massa.

b. Determine o momento de inércia em torno de um eixo que passa pela massa A e é perpendicular à página.

c. Determine o momento de inércia em torno de um eixo que passa através das massas B e C .

Passo 1

Fala galera, tudo bem?

Letra a)

Para calcular o centro de massa, precisamos das massas e das respectivas coordenadas, então a partir do desenho temos:

m a = 200 g

6 , h

m b = 100 g

0,0

m c = 100 g

12,0

A altura h é a altura do triângulo formado pela metade da base ( 6 c m ) e uma das hastes ( 10 c m ) . Então aplicando Pitágoras a altura é:

10 2 = h 2 + 6 2

h 2 = 10 2 - 6 2 = 100 - 36 = 64

h = 8 c m

As coordenadas do centro de massa ( x c m , y c m ) são:

x c m = x a m a + x b m b + x c m c m a + m b + m c

y c m = y a m a + y b m b + y c m c m a + m b + m c

Agora é só substituir. Primeiro vamos calcular o x c m :

x c m = 0,1.0 + 0,2.0,06 + 0,1.0,12 0,1 + 0,2 + 0,1 = 0,06 m

E agora para o y c m :

y c m = 0,1.0 + 0,2.0,08 + 0,1.0 0,1 + 0,2 + 0,1 = 0,04 m

Então as coordenadas do centro de massa são: ( 0,06 ; 0,04 )

Passo 2

Letra b)

Em relação ao eixo que passa por a , apenas as outras massas contribuem para o momento de inércia. A distância das massas até a é 10 c m e as massas valem 100 g cada. Nas unidades corretas, o momento de inércia é:

I = 0,1 0,10 2 + 0,1 0,10 2 = 0,002 k g m 2

Passo 3

Beleza até aqui?

Agora em relação a um eixo que passa através das massas B e C , a única massa que contribui é a a . A distância da massa a até o eixo x é 8 c m , a massa vale 200 g , então o momento de inércia é:

I = 0,2 0,08 2 = 0,00128 k g m 2

Beleza?

Espero ter ajudado!

Vamos pra próxima?

Resposta

a ) ( 0,06 ; 0,04 )

b ) 0,002 k g m 2

c ) 0,00128 k g m 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o sistema de quatro partículas da figura 9-45, (a) determine o momento de inércia I x em relação ao eixo x que passa por m 2 e m 3 e (b) determine o momento de inércia I y em relação ao eixo y qu
A molécula de metano ( C H 4 ) possui quatro átomos de hidrogênio localizados nos vértices de um tetraedro regular de 0,18 n m de lado, com o átomo de carbono no centro do tetraedro (figura 9-48). Det
Um corpo maciço de massa m , colocado sobre uma superfície horizontal sem atrito, está preso a um fio que é enrolado em torno de um pilar cilíndrico vertical preso à superfície. Assim, quando o corpo
O momento de inércia da Terra em relação ao seu eixo vale, aproximadamente, 8,03 × 10 37 k g ⋅ m 2 . (a) Como a Terra é quase esférica, suponha que seu momento de inércia possa ser escrito como I = C
56. Determine o momento de inércia em torno do eixo do objeto mostrado na FIGURA P12.56.