Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 16.1 - Ex. 79
Três ondas, que têm a mesma frequência, o mesmo comprimento de onda e a mesma amplitude, viajam ao longo do eixo . As três ondas são descritas pelas seguintes funções de onda: , onde está em metros e está em segundos. A função de onda resultante é dada por . Quais são os valores de e de ?
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Vamos esboçar um diagrama para o sistema. Assim podemos entender melhor o problema:
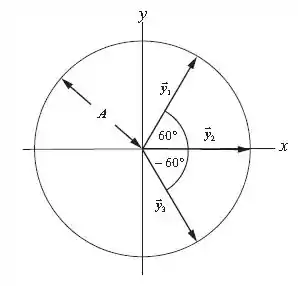
De acordo com o diagrama, fica evidente que:
A soma das componentes em , é dada por:
A magnitude resultante é dada por:
A direção do vetor resultante é dada por:
Resposta
Exercícios de Livros Relacionados
Uma onda tem uma velocidade de 240 m s e um comprimento de onda de 3,2m . Qual é (a) a frequência e (b) o período da onda?
Uma onda senoidal transversal que se propaga no sentido positivo de um eixo x tem uma amplitude de 2,0c m . um comprimento de onda de 10c m e uma frequência de 400H z . Se a equação da onda é da forma
A velocidade no vácuo das ondas eletromagnéticas (como as ondas de luz visível, as ondas de rádio e os raios X) é 3,0 × 10 8m / s . (a) Os comprimentos de onda da luz visível vão de aproximadamente 40
Velocidade de propagação da onda versus velocidade de uma partícula. (a) Mostre que a Equação 15.3 pode ser escrita na forma y x , t = A cos 2 π λ x - v t (b) Use y ( x ,t ) para encontrar uma expre
Uma onda em uma corda é descrita por y x , t = A c o s ( k x - ω t ) , Faça gráficos para y ,v yea y em função de x para t = 0 .Considere os seguintes pontos sobre a corda: x = 0 ; x = π / 4 k ; x = π