As cargas e coordenadas de duas partículas mantidas fixas no plano são , , e , , . Determine (a) o módulo e (b) a orientação da força eletrostática que a partícula exerce sobre a partícula . Determine também (c) a coordenada e (d) a coordenada de uma terceira partícula de carga para que a força exercida sobre a partícula pelas partículas e seja nula.

c) Agora, o esquema muda, por que foi inserida uma carga na história. As letras e querem as coordenadas dessa carga para que a força total que a carga sente seja nula. Para isso, vamos, primeiro, desenhar o sistema, colocando em um ponto com coordenadas aleatórias:

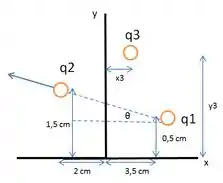
A primeira regra de ouro aqui é: para que a força total sobre seja nula, é necessário que as cargas estejam sobre uma mesma reta. Então, na verdade, a gente tem esse sistema que corresponde ao equilíbrio de :

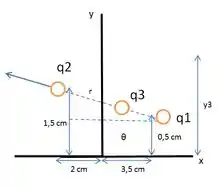
Agora, vamos chamar de a distância entre e . Para que esteja em equilíbrio, as forças exercidas pelas partículas e sobre elas devem ser iguais em módulo. Então, temos que:

Concordamos que podemos cancelar termos que se repetem dos dois lados nos numeradores, correto? Então vamos cortar as constantes e o módulo da carga :

Subsituindo o valor das cargas por: e , ficamos com:

Isolando o de um lado:

Vamos realizar essas operação então:

Retirando a raiz quadrada de ambos os lados, ficamos com:

Como se trata da distância entre dois pontos e não coordenadas. Então deve ser positivo:

Tranquilo até aqui? 😎

Agora, pra gente encontrar basta usarmos essa relação, baseada na figura mostrada no passo anteior. Mas, antes de tudo, veja que é necessário que possua coordenada negativa, pois como tanto a carga 3 quanto a carga 1 são positivas, elas devem estar em lados opostos da carga 2 para que assim o as forças que e exercem sobre a carga se anulem:

Vamos olhar pra seguinte figura:

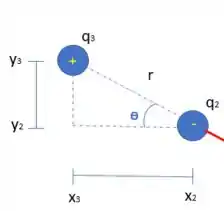
Dessa forma, temos que:

Logo:

Substituindo os valores que encontramos:

Bacana, não é? 😊

Para encontrar , basta a gente usar a relação:

Substituindo os valores que já sabemos:

E aí! entendeu tudo? Responde Aí! 😁