Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 21.4 - Ex. 16
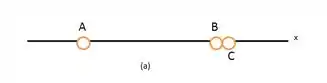
Na Fig. 21-29a, três partículas positivamente carregadas são mantidas fixas em um eixo . As partículas e estão tão próximas que as distâncias entre elas e a partícula podem ser consideradas iguais. A força total a que a partícula está submetida devido à presença das partículas e é N no sentido negativo do eixo . Na Fig. 21-28 b, a partícula foi transferida para o lado oposto de , mas mantida à mesma distância. Nesse caso, a força
total a que a partícula está submetida passa a ser no sentido negativo do eixo . Qual é o valor da razão ?
Passo 1
E aí, pessoal! 😉
Nesse problema temos três cargas alinhadas no mesmo eixo em duas situações diferentes. Na primeira as cargas e estão juntas de modo que a distancia para a carga é a mesma. Nesse caso a força que a força sofre é dada por
E quando passamos a partícula para o outro lado, a força aplicada na partícula A continua no mesmo sentido, porém ela passa a ser:
De começo você pode achar que a força aumentou né? Mas não, ela diminuiu, olha pra potência de 10 que acompanha a segunda força!
Se compararmos as duas forças acompanhadas pela mesma potência , vemos que:
Ou seja, a força diminuiu! Não aumentou, quando a partícula passou para o outro lado.
A partir dessas informações queremos saber qual é a razão .
Passo 2
Veja que, no primeiro caso, a força elétrica é proporcional a , pois ela é a soma das forças ocasionadas por e , que, nesse caso, está direcionada para a esquerda, como sabemos que as cargas são iguais se repelem.
Temos uma certeza: a soma das cargas tem o mesmo sinal que a carga . Show? Olha pra esse desenho aqui pra entender as forças atuando:
Já no segundo caso é diferente. Como a força continua direcionada no mesmo sentido, mas mais fraca, sabemos que a força que ocasiona em está direcionada para a direita, enquanto a força que exerce sobre está no sentido negativo de . Assim as forças se anulam um pouco:
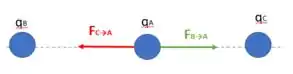
Como a força continua no mesmo sentido, a força que a carga gera em é maior que a força que gera em , logo:
Então, nesse caso, a força eletrostática total é proporcional a .
Tranquilo até aqui? 🤔
Passo 3
Usando essas considerações que a gente fez, encontramos a proporção entre:
Substituindo os valores das forças:
Achamos então a relação:
Multiplicando os dois lados por :
Aplicando a propriedade distributiva:
Vamos isolar tudo que tem para um lado e tudo que tem no outro:
Chegamos no nosso resultado final:
Usando essa equação, podemos encontrar:
E aí! o que achou? Responde Aí! 😁
