Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 2.Problemas - Ex. 4
Um tubo contendo ar comprimido a uma pressão de tem um vazamento através de um pequeno orifício em sua parede lateral. Sabendo que a densidade do ar na atmosfera é de , calcule a velocidade de escapamento do ar através do orifício.
Passo 1
Vamos começar com um desenho da situação:
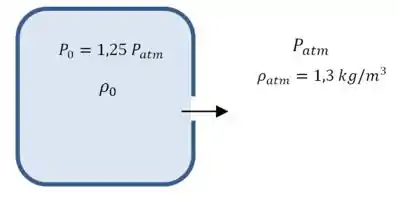
O enunciado deu o valor da densidade do ar (do lado de fora). Vamos começar encontrando uma relação entre essa densidade e a pressão.
Usando a lei dos gases ideais:
Mas o número de mols pode ser escrito como (onde é a massa do gás e é a massa molar):
Beleza, fizemos a densidade aparecer. O termo entre parênteses é constante entre os dois ambientes:
Passo 2
Agora vamos usar essa relação entre densidade e pressão para determinar a densidade do gás dentro do tubo:
Beleza, então agora temos os seguintes valores:
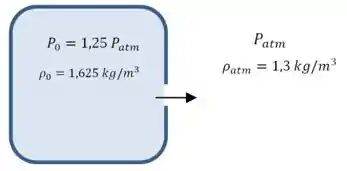
Agora falta calcular as velocidades.
Passo 3
Vamos usar a equação de Bernoulli. Tomando um ponto dentro do tubo e outro no orifício por onde o gás sai:
Perceba que o ponto no orifício está em contato com a atmosfera, por isso usamos do lado direito da equação.
Podemos escolher os dois pontos de forma que :
No ponto dentro do tubo temos e :
Usando :
Resposta
A velocidade de escapamento do ar é .