Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 1.Problemas - Ex. 11
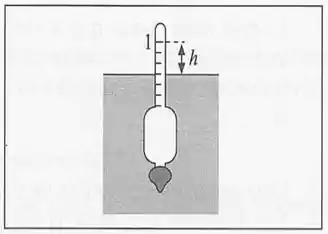
11. Um densímetro tem a forma indicada na figura. , com uma haste cilíndrica graduada, ligada a um corpo que geralmente contém algum lastro. O densímetro é calibrad, mergulhando-o na água, marcando com a graduação a altura na haste até a qual a água sobe e determinando o volume do densímetro situado abaixo da marca ( ou seja, o volume total que fica mergulhado na água). Seha a altura da qual a haste entre a graudação e o nível até onde o densímetro mergulha quando colocada num líquido de densidade desconhecida (Fig ). Calcule a densidade relativa desse líquido em relação a água, em função de , e .
Passo 1
Bora lá pra mais um probleminha de hidrostática nesse maravilhoso e complicado livro de Física.
Após a imersão do densímetro na água e calibração o volume abaixo da graduação “” é , que é também o volume submerso. Sendo assim, como o empuxo se iguala à força peso do densímetro, temos que:
Onde representa a densidade do densímetro, seu volume total e representa a densidade da água. Após ser mergulhado em outro líquido de densidade , o densímetro se eleva a uma altura em relação a marca , e o volume submerso passa a ser . Igualando o empuxo ao peso, obtemos que:
Passo 2
Só que anteriormente, no , obtemos que:
O que nos leva à seguinte identidade:
Que maravilha! Chegamos a relação que queríamos, pois afinal de contas a densidade relativa entre o líquido e a água nada mais é do que a razão :
Pronto! Tá na mão a resposta!