Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 14.7 - Ex. 64
Na figura, a água atravessa um cano horizontal e sai para a atmosfera com uma velocidade . Os diâmetros dos segmentos esquerdo e direito do cano são e . (a) Que volume de água escoa para a atmosfera em um período de ? Quais são (b) a velocidade e (c) a pressão manométrica no segmento esquerdo do tubo?
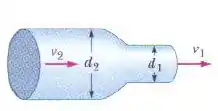
Passo 1
Falaaa galerinha bonita, tudo beleza?
Saca só, nesse exercício aqui, a letra (a) quer saber qual volume de água sai do tubo em . Vamos prestar atenção nas unidades de medida pra ver se dá pra resolver isso de forma fácil.
Primeiro precisamos lembrar da equação da continuidade, dada como:
O que é esse produto de área com velocidade? Vamos dar olhadinha nas unidades de medida: a área é medida em metros quadrados () e a velocidade em metros por segundo (), quando multiplicamos os dois:
Achamos metros cúbicos por segundo! Ou seja, é o volume de água que se desloca a cada segundo.
Passo 2
Beleza, agora já sabemos como medir a quantidade de volume por segundo, é só multiplicar a área do cano pela velocidade da água nesse lugar.
A área da boca do cano é:
Logo:
Multiplicando pela velocidade temos:
Ou seja, a cada segundo, saem pelo cano.
Como são , a quantidade final de água que vai ter saído depois desses vai ser:
Passo 3
A letra (b) quer que a gente encontre a velocidade da água na parte mais grossa do cano. Aqui a gente pode usar a equação da continuidade, já até calculamos um dos seus termos:
Isolando
Pronto.
Passo 4
E a letra (c) quer a pressão manométrica do lado esquerdo do tubo.
Lembrando que a pressão manométrica é dada como:
Sendo assim, vamos encontrar a pressão absoluta e depois subtrair da pressão atmosférica.
E para encontrar a pressão?
Não tem erro: questão de fluidos comparando pressão, velocidade e/ou altura de dois pontos? Equação de Bernoulli:
Vamos reorganizar isso:
Mas olhando pro cano, dá pra ver que ele é reto, ou seja, não tem nenhuma variação de altura, logo . Aí fica:
Além disso, como o lado direito tem saído pro ar, a pressão ali é igual à pressão atmosférica, então . (É muito comum ter que usar isso em questões de fluidos, então guarde bem).
Como a densidade da água é .
Agora pra acabar precisamos encontrar a pressão manométrica. De modo que:
Resposta
(a)
(b)
(c)