Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 6.Problemas - Ex. 73
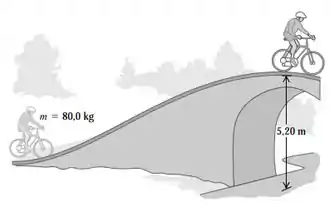
Você e sua bicicleta possuem massa total igual a 80,0 kg. Quando você atinge a base de uma ponte, está se deslocando com uma velocidade de 5,0 m/s. No topo da ponte você subiu uma distância vertical de 5,20 m e sua velocidade diminuiu para 1,50 m/s. Despreze o trabalho realizado pelo atrito e qualquer ineficiência na bicicleta ou em suas pernas.
a) Qual o trabalho total realizado sobre você e sua bicicleta quando você vai da base ao topo da ponte?
b) Qual o trabalho realizado pela força que você aplica sobre os pedais?
Passo 1
Faremos utilizando a relação trabalho – energia da seguinte forma:
Sabendo então a fórmula da energia cinética, substituímos na equação acima:
Agora só nos resta substituir os valores e achar a resposta! Simples e rápido, não é verdade?
Calculando...
Passo 2
Nesse caso o trabalho pode ser desenvolvido pela subtração do trabalho feito pela força da gravidade e pelo trabalho da energia cinética, logo:
O trabalho realizado pela força da gravidade pode ser desenvolvido pela fórmula da energia potencial, teremos:
O trabalho da energia cinética nós já havíamos calculado na questão anterior e o sinal de negativo da energia potencial deve – se ao movimento estar indo contra a força gravitacional, no caso subindo.
Agora vamos resolver!
Passo 3
Resposta
a) O trabalho realizado é de – 910 Joules.
b) O trabalho realizado é de 3166,8 Joules.