Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 7.Problemas - Ex. 85
Uma força conservativa F atuando ao longo do eixo Ox e uma força dada pela lei de Hooke atuam sobre um íon.
a) Mostre que uma possível função energia potencial para a combinação dessas forças é dada por
Essa é a única função possível? Explique.
b) Ache a posição do equilíbrio estável.
c) Faça um gráfico de U(x) (em unidades de ) versus x (em unidades de ) para valores de x entre e .
d) Existe alguma posição de equilíbrio instável?
e) Quando a energia total for , qual será o valor máximo e o valor mínimo de x para o movimento do íon?
f) Sendo m a massa do íon, determine sua velocidade máxima quando a energia total for . Para qual valor de x sua velocidade é máxima?
Passo 1
Vamos utilizar a equação . O equilíbrio é estável onde U (x) é um mínimo local e o equilíbrio é instável onde U (x) é um máximo local.
Lembrando que é a inclinação do gráfico de U em função de x; e , então K é um máximo quando U é um mínimo. O máximo x é onde E = U.
Para
então essa é uma possível função potencial. Para esse potencial, , não zero.
Definir o zero de potencial é equivalente a adicionar uma constante ao potencial; qualquer constante aditiva não mudará a derivada e corresponderá à mesma força.
No item (b), para o equilíbrio, a força é zero. Então,
Como , então
No item (c), temos o seguinte gráfico
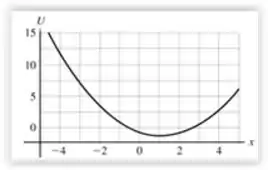
No item (d), o equilíbrio estável é apenas em um ponto de , por isso, não há outra localização.
No item (e), para um valor máximo e mínimo de x, temos que os valores extremos de x correspondem à velocidade zero, portanto, energia cinética zero, então
Resolvendo o quadrático, temos
Então, é igual a
Logo,
Então, para x positivo e negativo, temos
Para o item(f), a energia cinética máxima ocorre quando U (x) é mínimo, então, usando o ponto , podemos fazer
Então,
Resposta
a)
b)
c) gráfico.
d) não há outra localização.
e) e
f)