Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 1.Problemas Adicionais - Ex. 57
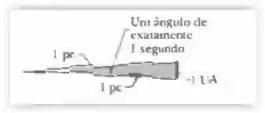
A unidade astronômica () é a distância média entre a Terra e o Sol, cerca de milhas. O parsec () é a distância para a qual uma distância de subtende um ângulo de exatamente segundo de arco (Fig. 1-8). O ano-luz é a distância que a luz, viajando no vácuo com uma velocidade de milhas por segundo, percorre em ano. Expresse a distância entre a Terra e o Sol :
(a) em parsecs .
(b) em anos-luz .
Passo 1
Então galera , a primeira coisa que temos que observar é que quando é obtido em radianos , podemos achar seu valor simplesmente dividindo o arco pelo raio . Caso você não se lembre muito bem dessa propriedade , vamos ilustrar a seguir:
Onde:
Voltando à questão, podemos concluir que , para um raio muito grande e um pequeno valor de , o arco pode ser aproximado por segmento de reta de comprimento . Precisamos dar uma olhada nas relações que conhecemos antes de fazermos as conversões:
Agora precisamos converter o valor de para radianos, para que possamos jogar na fórmula e obter o valor do parsec. Podemos fazer a conversão de para através da relação:
Passo 2
Agora que obtivemos o ângulo em radianos, podemos obter o valor do parsec () através da fórmula:
Tal que:
Agora que temos o valor do parsec dado em podemos calcular a distância em parsecs através da relação:
Passo 3
Agora para obtermos a distância entre a terra e o sol precisamos primeiramente calcular quantos segundos existem em ano. Temos que:
Além disso, sabemos que:
Logo:
Em seguida, sabendo que milhas, podemos achar a distância entre o sol e a terra em anos-luz através da fórmula:
Resposta
As respostas assustam mas é isso mesmo pessoal!!! Partiu resolver mais questões???