Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 10.1 - Ex. 31
Uma partícula se move em um cirulo centrado na origem. A posição da partícula é e sua velocidade angular é . (a) Mostre que sua velocidade é dada por . Mostre que sua aceleração centrípeta é dada por
Passo 1
Essas formulas que vamos mostrar são bem importantes, então é interessante que você as memorize!
a) Vamos considerar o seguinte:
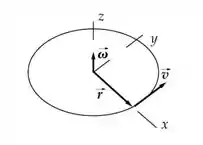
Nosso vetor no plano e saindo do plano, isto é, no eixo !
Passo 2
As coisas vão ficar assim ó:
Como aponta para o direção positiva de :
E aponta para o direção positiva de :
Logo,
Isto é:
Passo 3
Para o item (b):
A brincadeira que fizemos ali em cima foi tipo uma a regra do produto lá de derivada 😉
Continuando, temos:
Lembrete:
Como
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Para t = 0 a corrente de um motor elétrico de corrente contínua ( d c ) é invertida, produzindo um deslocamento angular do eixo do motor dado por θ t = 250 t - 20 t 2 - 1,5 t 3 .a) Em que instante a v
a) Calcule o ângulo em radianos subtendido por um arco de 1,5 m de comprimento ao longo de uma circunferência de raio igual a 2,5 m . Qual é esse ângulo em graus? b) Um arco de comprimento igual a 14
Uma criança está empurrando um carrossel. O deslocamento angular do carrossel varia com o tempo de acordo com a relação θ t = γ t + β t 3 , onde γ = 0,4r a d / s e β = 0,012r a d / s 3 .a) Calcule a v
A velocidade angular de um volante obedece à equação ω z t = A + B t 2 , onde t está em segundos e A e B são constantes, com valores numéricos de 2,75( p a r aA ) e 1,5( p a r aB ) . a) Quais são as u
O ângulo descrito por uma unidade de disco girando é dado θ t = a + b t - c t 3 , onde a , b e c são constantes positivas tais que se t for dado em segundos, θ deve ser medido em radianos.Quanto t = 0