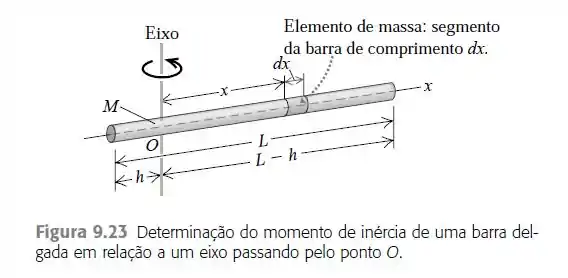
Usando o teorema dos eixos paralelos e informações da Tabela 9.2, ache o momento de inércia da barra delgada de massa M e comprimento L indicado na Figura 9.23 em relação a um eixo passando pelo ponto O situado a uma distância arbitrária h de uma de suas extremidades. Compare seu resultado com o encontrado no Exemplo 9.11 (Seção 9.6).
Passo 1
A figura é:
Temos que o teorema do eixo paralelo é:
Sabemos que o momento de inercia da barra delgada é:
E que:
Passo 2
Dessa forma, temos que:
Passo 3
Comparando com o exemplo 9.11:
Bom, nós obtemos o mesmo resultado.
O exemplo 9.11 mostra que esse resultado fornece o resultado esperado para , e .