Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 18.1 - Ex. 95
- Use os resultados do Problema 94 para mostrar que, no limite que , o modelo de Einstein fornece a mesma expressão para calor específico que a lei de Dulong-Petit.
- Para o diamante, é aproximadamente 1060 K. Integre numericamente para determinar o aumento da energia interna se 1,00 mol de diamante é aquecido de 300 a 600 K.
Passo 1
Legal pessoal, na letra a temos que usar o resultado do exercício anterior.
O problema 94 nos forneceu uma equação para o calor específico molar:
Para achar o limite quando , a primeira coisa que devemos fazer é simplificar ao máximo a equação eliminando a indeterminação, já que neste caso o denominador será próximo de zero.
Vamos começar abrindo o denominador:
Dividimos tudo por
Então:
Expressando os termos exponenciais em suas séries de potências:
Substituindo:
Então o modelo de Einstein fornece a mesma expressão para calor específico que a lei de Dulong-Petit
Passo 2
Terminamos uma, agora vamos para a próxima. Temos a equação para o calor específico molar:
Mas queremos a variação da energia interna, que será dada por:
Temos e que T varia de 300 K até 600K.
Agora vamos pensar, de acordo com o que já aprendemos em cálculo se fizermos um gráfico de versus T, a área abaixo da função formada nos fornecerá a variação da energia interna.
Primeira coisa, vamos montar uma tabela relacionando estas temperaturas com seus respectivos calores específicos:
Agora vamos fazer um gráfico, o excel mesmo nos permite fazê-lo:
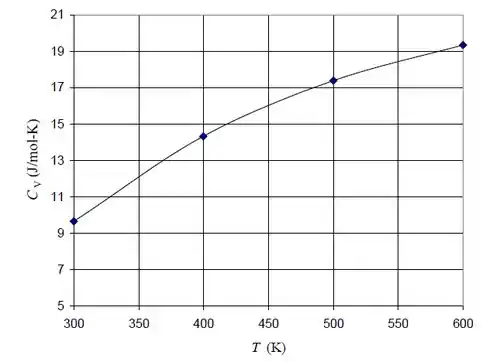
A linha não é reta ao longo de toda a variação, mas entre as temperaturas de 300K e 400K, 400K a 500K e 500K e 600K temos linhas retas unindo os pontos, formando um trapézio. Então para achar a área total vamos somar a área de todos os três trapézios formados.
Lembrando que:
Então:
Sabemos que o problema quer saber a variação da energia interna para 1 mol, então: