Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 4.6 - Ex. 45
Quando vê um inseto pousado em uma planta perto da superfície da água, o peixe-arqueiro coloca o focinho para fora e lança um jato d'água na direção do inseto para derrubá-lo na água (Fig. 4-38). Embora o peixe veja o inseto na extremidade de um segmento de reta de comprimento d, que faz um ângulo com a superficie da água, o jato deve ser lançado com um ângulo diferente, , para que o jato atinja o inseto depois de descrever uma trajetória parabólica. Se , e a velocidade de lançamento é , qual deve ser o valor de para que o jato esteja no ponto mais alto da trajetória quando atinge o inseto?
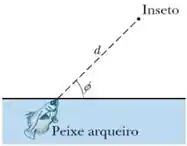
Passo 1
Belezoca galerinha, de acordo com o enunciado, teremos que a posição do inseto em relação ao peixe vai ser descirta através das componentes;
Logo:
Passo 2
Como queremos que o inseto esteja exatamente no ponto mais alto da trajetória do jato de água que o peixe disparou, teremos que a altura dessa trajetória será dada como:
Onde é o ângulo que o jato do peixe faz com a superfície da água:
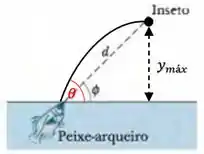
Dessa forma, vamos obter que:
Subsituindo os valores que o enunciado nos fornece:
Portanto:
Resposta
Beleza , galera ? Bora fazer mais exercícios então!!!