Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 97
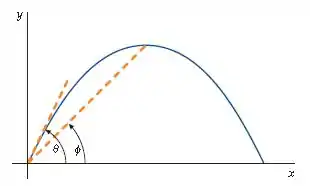
Um projétil é lançado a um ângulo acima do nível do chão. Um observador, parado no ponto de lançamento, vê o projétil em seu ponto de altura máxima e mede o ângulo mostrado na Figura 3-38. Mostre que .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Vamos lá provar o que foi proposto pelo enunciado:
Sabemos que:
Por Torricelli temos:
Adotando a velocidade final, no ponto de altura máxima, nula, temos:
Substituindo na nossa primeira equação, temos:
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Um projétil é lançado com velocidade v 0 formando um ângulo α 0 com a horizontal. O ponto de lançamento está situado a uma altura h acima do solo. Desprezando a resistência do ar, mostre que a distânc
Um taco golpeia uma bola de golfe em uma pequena elevação acima do solo com uma velocidade de 12,0 m/s e um ângulo inicial de 51,0 ° acima da horizontal. A bola atinge o campo 2,08s após a tacada. Des
Uma pedra é atirada do telhado de um edifício com velocidade v 0 , formando um ângulo α 0 com a horizontal. Despreze a resistência do ar. Determine o módulo, a direção e o sentido da velocidade da ped
a) Prove que um projétil lançado em um ângulo α 0 possui o mesmo alcance horizontal de outro lançado com a mesma velocidade em um ângulo ( 90 ° - α 0 ) . b) Uma rã salta com uma velocidade de 2,2m / s
Uma bola de 2,7k g é jogada de baixo para cima com velocidade inicial de 20m / s , da borda de um rochedo que mede 45,0m de altura. No instante em que a bola é jogada, uma mulher começa a correr da ba