Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 1.Problemas - Ex. 90
Ângulo da ligação no metano. Na molécula do metano, CH4, cada átomo de hidrogênio ocupa o vértice de um tetraedro regular em cujo centro se encontra o átomo de carbono. Usando coordenadas de tal modo que uma das ligações esteja na direção , uma ligação adjacente estará na direção . Calcule o ângulo entre estas duas ligações.
Passo 1
Oi, galerinha! Tudo bom?
Vamos começar desenhando a molécula do metano. A bolinha preta representa o átomo de carbono e as brancas ligadas a ela são os hidrogênios.
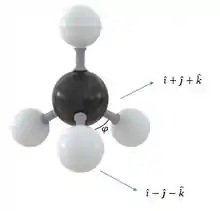
Como foi dito no problema, considerando que uma ligação está na direção , a ligação adjacente, ou seja, a do lado estará na direção e queremos saber o ângulo, que eu chamei de , entre essas duas ligações.
Se pensarmos nas ligações como vetores, podemos usar o produto escalar para calcular esse ângulo.
Veja só!
Passo 2
Para resolver essa questão, nós temos duas definições para o produto escalar.
Uma delas é a 1.21:
E a equação 1.18:
O que precisamos fazer é achar o produto escalar através da equação 1.21 e depois igualar à equação 1.18 pra achar o cosseno do ângulo entre eles e, consequentemente, o ângulo.
Animado? Então bora!
Passo 3
Para o nosso problema vamos considerar como sendo a nossa primeira ligação:
E como sendo a ligação adjacente:
Vamos usar a equação 1.21, lembrando que o vetor unitário está relacionado ao eixo , o vetor unitário está relacionado ao eixo e o vetor unitário está relacionado ao eixo .
Tranquilo até aqui?
Passo 4
Para igualarmos a equação 1.18, precisaremos achar os módulos de e , usando a fórmula do módulo de um vetor.
Começando por :
E agora :
Bacana, não é?
Passo 5
Já temos os módulos de e , só falta igualar o resultado da equação 1.21 à equação 1.18:
Estamos quase lá!
Passo 6
Agora é só usar o arco-cosseno pra encontrar o ângulo. O que quer dizer que vamos nos perguntar: Qual o ângulo que tem o cosseno igual a ? Podemos procurar isso na calculador e encontraremos:
E achamos o ângulo, pimpolho!
Entendeu tudo? Responde Aí! 😉
Resposta
109°