Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 2.10 - Ex. 65

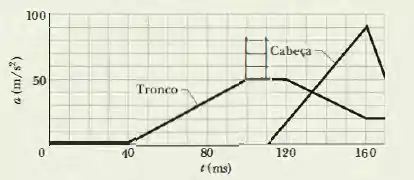
A Figura 2-13 mostra a aceleração da cabeça e do tronco de um voluntário durante urna colisão frontal. Qual é a velocidade (a) da cabeça e (b) do tronco quando a aceleração da cabeça é máxima?

Passo 1

Galera, sabemos que a área entre o gráfico da aceleração e o eixo t é numericamente igual a variação da velocidade. Cada quadradinho de unidade de t equivale a 10   ms = 10 × 10 - 3 s , enquanto cada quadradinho de unidade de aceleração vale 10   m/ s 2 .

A aceleração da cabeça é máxima em t = 160   ms , por isso a variação da velocidade vai ser a área do triangulo que é formado.

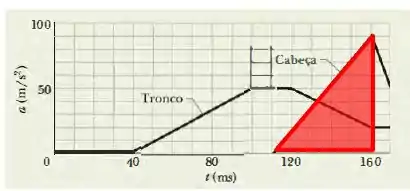
Logo, a área desse triangulo será dada como:

Δ v c = 1 2 90   m/ s 2   . 160 × 10 - 3   s - 110 × 10 - 3   s

∆ v c = 2,25   m/s

Passo 2

Para o tronco vamos fazer o mesmo, mas vamos ter que dividir em mais regiões. A primeira região vai ser um triângulo que vai de 40   ms até 100   ms ; a segunda vai ser um retângulo de 100   ms até 120   ms ; já a terceira vai ser um trapézio que vai de 120   ms até 160   ms .

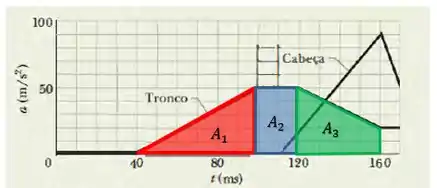
Sendo assim, obtemos que:

A 1 = 50   m/ s 2 . 100 × 10 - 3   s - 40 × 10 - 3   s 2 = 1,50   m/s

A 2 = 120 × 10 - 3   s - 100 × 10 - 3   s 50   m/s² = 1,00   m/s

A 3 = 50   m/ s 2   + 20   m/ s 2   160 × 10 - 3   s - 120 × 10 - 3   s 2 = 1,40   m/s

Portanto, a variação de velocidade será:

Δ v = A 1 + A 2 + A 3

∆ v = 1,50   m/s + 1,00   m/s + 1,40   m/s

∆ v = 3,90   m/s

Resposta

a) 2,25   m / s

b) 3,90   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A Fig. 2-41 mostra a aceleração a em função do tempo t para uma partícula que se move ao longo do eixo x . A escala vertical do gráfico é definida por a s = 12,0m / s 2 . No instante t=- 2,0s , a velo
Um trem partiu do repouso com aceleração constante. Em um certo instante, estava se movendo a 30m / s ; 160m adiante, estava se movendo a 50m / s calcule:(a) a aceleração, (b) o tempo necessário para
Deixa-se cair uma pedra, sem velocidade inicial, do alto de um edifício de 60m . A que distância do solo está a pedra 1,2s antes de chegar ao solo?
Uma partícula parte da origem em t = 0 e se move no sentido positivo do eixo x . O gráfico da velocidade da partícula em função do tempo é mostrado na Fig. 2-43; a escala vertical é definida por v s =
Um carro que se move com aceleração constante percorreu em 6,00s a distância de 60,0m que separa dois pontos. A velocidade do carro ao passar pelo segundo ponto era 15,0m / s . (a) Qual era a velocida