Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 1.9 - Ex. 50
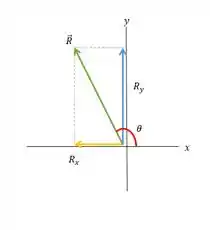
Dados dois vetores e a) ache o módulo de cada vetor; b) escreva uma expressão para a diferença vetorial usando vetores unitários; c) ache o
módulo e a direção diferença vetorial ; d) faça um diagrama vetorial para e e mostre que os resultados concordam aproximadamente com a resposta do item c).
Passo 1
Oi, galerinha!
Nesse problema temos dois vetores e e nosso objetivo é obter o modulo de cada vetor escrever uma expressão para a diferença vetorial usando vetores unitários e obter o modulo e a direção desse vetor resultante.
Parece complicado? 👀
Veja só! 😊
Passo 2
Para resolver a letra a temos que decompor as componentes de e , e depois achar o módulo.
Vamos precisar lembrar que um vetor pode ser escrito em termos de suas componentes e de maneira que:
Então se,
Logo,
Para calcular o seu módulo usamos a seguinte relação:
Assim, substituindo, ficamos com:
E esse é o módulo do vetor
Agora, vamos decompor as componentes de :
Tranquilo até aqui? 😉
Passo 3
Agora que a gente já sabe o módulo, vamos calcular a diferença vetorial dos verotes enunciados, ou seja, vamos usar os componentes encontrados na letra a.
Bacana, não é? 😊
Passo 4
Na letra b, já encontramos o valor de
Agora é seguir o mesmo raciocínio da letra a. Vamos decompor as componentes de :
E seu módulo:
Estamos quase lá! 😬
Passo 5
Vamos calcular a direção do vetor :
Sabemos que para isso, vamos utilizar a relação:
E sabemos que:
Então:
Como o ângulo está em sentindo negativo, fazemos que:
Saca só! 😁
Passo 6
Como e , então a resultante, , se encontra no segundo quadrante.
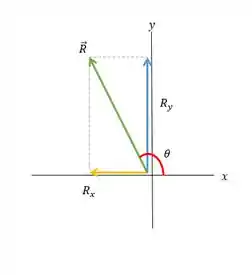
E aí! o que achou? Responde Aí! 😇
Resposta
