Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 3.Problemas Adicionais - Ex. 45

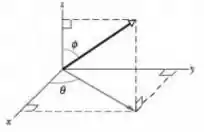
Os vetores e estão no plano . tem módulo e ângulo ; tem componentes e . (a) Determine . Determine (b) em termos dos vetores unitários e (c) através do módulo e do ângulo em coordenadas esféricas (veja a Fig. 3-34). (d) Determine o ângulo entre os vetores . (Sugestão: pense um pouco antes de iniciar os cálculos). Determine (e) em termos dos vetores unitários e (f) através do módulo e do ângulo em coordenadas esféricas.

Passo 1

Na notação dos vetores unitários, os dois vetores são:

Passo 2

O produto escalar pedido pode ser calculado da seguinte forma:

Passo 3

Na notação dos vetores unitários, sabemos que:

Passo 4

Nós sabemos que o ângulo azimutal não é definido para vetores cujo ângulo polar é zero , sendo assim , a resposta correta para este item é:

Passo 5

Sabendo que está no plano e é perpendicular ao plano , podemos observar queo ângulo formado entre eles, por definição é

Passo 6

Em termos de vetores unitários, obtemos que:

Passo 7

De acordo com o teorema de Pitágoras, temos que . O ângulo azimutal, por sua vez, é , como no enunciado do problema é a projeção no plano do novo vetor que foi criado no item (e), temos que o ângulo polar é:

De boa pessoal???? Bora fazer mais exercícios então!!!!!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache o ângulo entre cada par de vetores:c) A → = - 4,0i ^ + 2,0j ^ e B → = 7,0i ^ + 14,0j ^ ;

Para os vetores indicados na Figura 1.35, a) ache o módulo e a direção do produto vetorialA → × B → ; b) ache o módulo e a direção do produto vetorial B → ×A → .

Encontre o produto vetorial A → × B → (expresso em termos dos vetores unitários) dos vetores indicados no Exercício 1.50. Qual o módulo deste produto vetorial?

Por meio de desenhos simples dos produtos vetoriais apropriados, demonstre que b) | A → × B → | pode ser interpretado como o produto do módulo de A → vezes o componente de B → perpendicular a A → , ou

Para os vetores A → e D → indicados na Figura 1.34, a) ache o módulo e a direção do produto vetorial A → × D → ; b) ache o módulo e a direção do produto vetorial D → × A → .