Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 3.Problemas Adicionais - Ex. 54
Para os vetores da Fig. 3 .32, com , e , calcule (a) , (b) e (c)
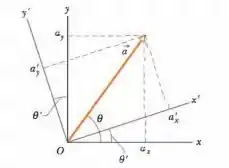
Passo 1
Então galera , podemos perceber pela figura que e .
Dessa forma :
Devemos lembrar que o produto vetorial entre dois vetores perpendiculares é zero, okay?
Passo 2
Precisamos calcular . Sabemos que :
Passo 3
Precisamos calcular . Sabemos que :
De boa , galera?? Bora resolver mais questões então
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Uma partícula se move em um círculo centrado na origem, a magnitude de seu vetor posição r → sendo constante. (a) Derive r → ∙ r → = r 2 = c o n s t a n t e em relação ao tempo, para mostrar que v → ∙
Dois vetores aeb são tais que a + b = a - b . Qual é o ângulo entre aeb ?
Calcule o ângulo entre duas diagonais internas (que passam por dentro) de um cubo, utilizando o produto escalar entre vetores.
O produto escalar de dois vetores unitários perpendiculares deve ser sempre zero? Um corpo tem uma velocidade v → em um dado instante. Interprete fisicamente v → . v → .Uma bola rola para fora de uma
Verdadeiro ou falso: (a) O produto escalar não pode ter unidades. (b) Se o produto escalar de dois vetores diferentes de zero for zero, eles serão paralelos. (c) Se o produto escalar de dois vetores d