Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 62
Uma viga rígida com de comprimento e massa de é apoiada em cada extremidade. Um estudante de encontra-se em pé a do suporte 1. Que valor de força cada suporte exerce sobre a viga?
Passo 1
Bom, vamos usar o desenho do enunciado para sabermos onde cada força atua:
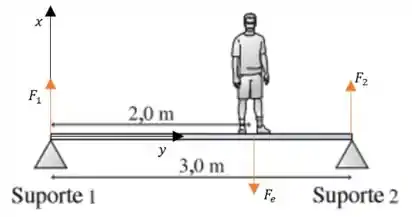
Agora consideramos que o nosso sistema de coordenadas tem sua origem no ponto de aplicação da força do Suporte 1 e o eixo de rotação vamos colocar no centro de massa da viga (poderia ser qualquer outro ponto para este caso, já que ela não rotaciona). Vamos usar a segunda lei de Newton para o caso rotacional:
Como a viga não rotaciona em nenhum sentido, a soma dos torques é zero. Se a gente considerar que o sentido positivo de rotação é o anti-horário, a soma dos torques fica:
Sendo que o último termo do lado esquerdo se refere ao estudante. Além disso, não consideramos o peso da viga no problema, porque como dissemos antes, o eixo está no centro de massa.
Passo 2
Sabemos a posição do estudante e a posição do centro de massa da viga, então sabemos o valor de todas as distancias entre os pontos de aplicação das forças e o centro de massa:
Isso porque os suportes estão nas extremidades da viga que tem , e o centro de massa está no meio da barra. E:
Que é a diferença da posição do centro de massa com a posição do estudante.
O peso do estudante vai ser:
Substituindo a massa que foi dada no enunciado e :
Passo 3
O problema é que as forças e são diferentes, e a gente só tem uma equação até agora, que encontramos no passo 1. Como precisamos de mais uma, vamos usar a segunda lei de Newton:
Como o centro de massa da barra não se desloca, então a segunda lei precisa ser igual a zero.
Agora a gente substitui todas as forças conforme o diagrama:
Repare que agora consideramos a força peso da viga, já que se trata do somatório das forças sobre o corpo e não dos torques!
Vai ficar o seguinte:
Passo 4
Pronto, temos duas equações para duas forças, então podemos resolver o sistema, começando pela última equação:
E agora substituímos na equação dos torques:
Por fim, a gente isola substitui as distancias que já sabemos e encontramos para depois achar :
Voltando na primeira equação para achar :