Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 79
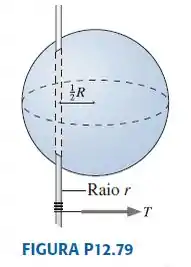
Uma esfera de massa M e raio R é rigidamente fixada a um bastão fino de raio r que passa por dentro dela, a uma distância R de seu centro. Um barbante é enrolado em torno do bastão e o puxa com uma tensão T. Determine uma expressão para a aceleração angular da esfera. O momento de inércia do bastão é desprezível.
Passo 1
A esfera presa a uma haste fina é um corpo rígido que gira em torno da haste. Suponha que a haste esteja vertical e a esfera sólida.
Vamos precisar consultar a Figura P12.79 (do enunciado). A esfera gira porque a corda enrolada na haste exerce um torque .
Passo 2
O torque exercido pela corda na haste é
A partir do teorema do eixo paralelo, o momento de inércia da esfera em torno do eixo da haste é:
Passo 3
Da segunda lei de Newton,
Resposta
Exercícios de Livros Relacionados
Considere uma transição de um estado mais baixo de energia para um estado mais alto – isto é, a absorção de um quantum de energia, resultando em um aumento da energia rotacional em uma molécula de N 2
Mostre que a diferença de energia entre um nível rotacional de uma molécula e o nível próximo mais alto é proporcional a l + 1 .
Você trabalha em um laboratório de pesquisa biomédica e está investigando os níveis rotacionais de energia da molécula de H B r . Após consulta à tabela periódica, você sabe que a massa do átomo de br
A separação de equilíbrio entre os núcleos da molécula de nitrogênio ( N 2 ) é 0,110 n m e a massa de cada núcleo de nitrogênio é 14,0 u , onde u = 1,66 × 10 - 27 k g . Para as energias rotacionais, a
Estrelas de nêutrons e restos de supernovas. A nebulosa do Caranguejo é uma nuvem de gás luminoso que possui uma extensão de 10 anos-luz, localizada a uma distância aproximadamente igual a 6500 anos-l