Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 16.1 - Ex. 87

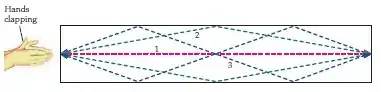
Se você bater palmas na extremidade de um longo tubo cilíndrico, o eco que você ouvirá não soará como palmas; o que você ouvirá soará como um assovio, no início com uma frequência muito alta, mas decaindo rapidamente até quase desaparecer. Este “assovio de galeria” pode ser explicado facilmente, se você pensar no som de um bater palmas como uma compressão isolada irradiando a partir das mãos. Os ecos do bater palmas que chegarem aos seus ouvidos terão viajado ao longo de diferentes caminhos dentro do tubo, como mostrado na figura 16-37. O primeiro eco a chegar terá feito um percuso reto de ida e volta no tubo, enquanto o segundo eco terá refletido uma vez no centro do tubo, tanto na ida quanto na volta, o terceiro eco terá refletido duas vezes em pontos a 1 / 4 e a 3 / 4 da distância, e assim por diante. O tom do som que você ouve corresponde à frequência com que estes ecos chegam aos seus ouvidos. (a) Mostre que o tempo que separa o n -ésimo eco do n + 1 -ésimo eco é

∆ t n = 2 v 2 n 2 r 2 + L 2 -   2 n - 1 2 r 2 + L 2  

Onde v é a rapidez do som, L é o comprimento do tubo e r é o raio do tubo. (b) Usando um programa de planilha eletrônica ou uma calculadora gráfica, plote ∆ t n   v e r s u s   n para L = 90,0   m e r = 1,00   m . Vá até pelo menos n = 100 . (c) Com seu gráfico, explique por que a frequência diminui com o tempo. Quais são as frequências mais alta e mais baixa que você ouvirá?

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Vamos esboçar um diagrama para o sistema. Assim podemos entender melhor o problema:

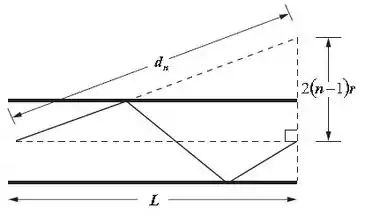
Aplicando o teorema de Pitágoras, temos:

d n = 2 4 n - 1 2 r 2 + L 2

O tempo de delay é dado por:

∆ t n = d n v

Substituindo, temos:

∆ t n = 2 v 2 n 2 r 2 + L 2 - 2 n - 1 2 r 2 + L 2

Passo 2

Item (b):

Abaixo está apresentado um esboço da planilha:

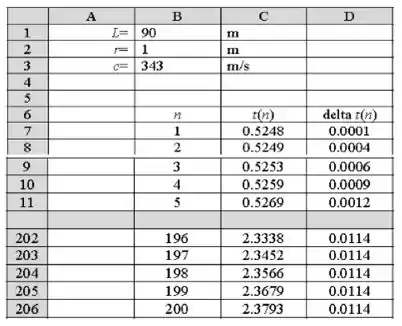
O gráfico obtido deve ser:

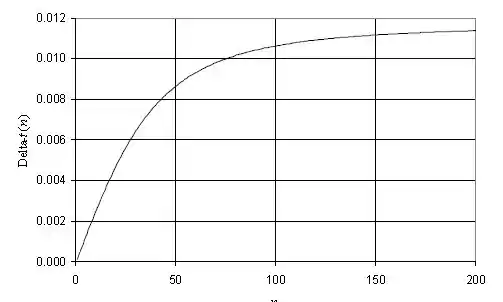
Passo 3

Item (c):

A maior frequência correspondente é dada por:

f = 1 ∆ t 1

f = v 2 2 2 r 2 + L 2 - L 2

Substituindo os valores, temos:

f = 343   m / s 2 4 ( 1   m ) 2 + ( 90   m ) 2 - 90   m

f = 7,72   k H z

A menor frequência é obtida através da análise do limite de ∆ t n para n → ∞ :

lim n → ∞ ⁡ ∆ t n = lim n → ∞ ⁡ 2 v 2 n r 2 + L 2 2 n 2 - 2 n - 1 r 2 + L 2 2 n - 1 2

  lim n → ∞ ⁡ ∆ t n = 2 r v 2 n - 2 n + 2 = 4 r v

Logo:

f ' = 1 ∆ t ∞ = v 4 r

Substituindo os valores, temos:

f ' = 343   m / s 4 ( 1   m )

f ' = 85,8   H z

Resposta

a ) ∆ t n = 2 v 2 n 2 r 2 + L 2 - 2 n - 1 2 r 2 + L 2

c ) f = 7,72   k H z

f ' = 85,8   H z

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma corda de violão é puxada pelo seu ponto médio. Um microfone em seu computador detecta o som e um programa do computador determina que a maior parte do som subsequente consiste em um tom de 100H z
Um tubo de órgão, sob condições normais, tem uma frequência fundamental de 220H z . Ele é colocado em uma atmosfera de hexafluoreto sulfúrico S F 6 , às mesmas temperatura e pressão. A massa molar do
Trabalhando para uma pequena mineradora de ouro, você se depara com um túnel de uma mina abandonada que, devido ao desmoronamento das escoras de madeira, parece muito perigoso para ser pessoalmente ex
Durante um experimento para estudar a rapidez do som no ar, usando um oscilador de áudio e um tubo aberto em uma ponta e fechado na outra, encontra-se uma particular frequência de ressonância com nós
O tubo da Figura 16-36 está cheio de gás natural [metano ( C H 4 ) ]. O tubo é pontilhado por uma linha de pequenos furos afastados de 1,00c m ao longo de todo o seu comprimento de 2,20m . Um alto-fal