Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 4.3 - Ex. 8
Você entra em um elevador, sobe em uma balança e aperta o botão para subir. Você se lembra que seu peso normal é . Desenhe um diagrama do corpo livre. (a) Quando o elevador tem uma aceleração para cima com módulo , qual é a leitura na balança? (b) Se você segurar um pacote de por um barbante vertical leve, qual será a tensão nesse barbante quando o elevador acelerar como na parte (a)?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente determinar a (a) leitura na balança quando a aceleração pra cima é e (b) a tensão no barbante que estiver segurando um pacote de dentro do elevador.
O elevador e tudo nele estão acelerando para cima, então vamos aplicar a segunda lei de Newton na direção vertical:
Sua massa é . Você e o pacote têm a mesma aceleração que o elevador. Então, seja subindo na direção da aceleração do elevador, vamos aplicar a segunda Lei o valor da força atuando em cada situação.
Vamos lá!
Passo 2
a) Seu diagrama de corpo livre é mostrado na figura a, onde é a força normal que aparece na leitura da balança.
Sendo assim, nos dá:
Onde é o peso de . Então, resolvendo para , temos:
E substituindo os valores:
Passo 3
b) O diagrama de corpo livre da embalagem é dado na figura b.
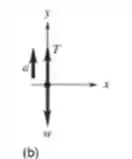
Sendo assim, usando a segunda lei de Newton para fazer o somatório das forças presentes, vamos ter:
Onde é a tensão no barbante:
E substituindo os valores, temos:
Os objetos aceleram para cima, então para cada um deles a força para cima é maior do que a força descendente.
Valeu, galera! Até a próxima! 😉