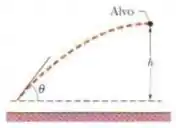
Você pretende atirar uma bola com uma velocidade escalar de em um alvo que está a uma altura acima do núvel do qual você vai lançar a vola (veja a figura). Você quer que a velocidade da bola seja horizontal no instante em que ela atinge o algo. (a) Com que ângulo acima da horizontal você deve atirar a bola? (b) Qual é a distância horizontal do ponto de lançamento até o alvo? (c) Qual é a velocidade escalar da bola no momento em que atinge o alvo?

(a) E como podemos usar essa informação para calcular o ângulo de lançamento.

Bom, se o módulo da velocidade inicial é , e ela forma um ângulo com a horizontal, a componente da velocidade inicial vertical é:

(b) Agora queremos calcular a distância horizontal entre a bola e o alvo.

Para isso, primeiro precisamos calcular o tempo que a bola leva para atingir o alvo. Vamos fazer isso usando o que já sabemos sobre a velocidade vertical:

Como já sabemos o ângulo de lançamento, podemos calcular a magnitude da velocidade horizontal, e então calcular a distância percorrida pela bola nesse intervalo de :

(c) Já vimos que, no instante em que a bola atinge o alvo, a velocidade é totalmente horizontal, ou seja:

Isso quer dizer que, para calcular o módulo da velocidade nesse instante, só precisamos olhar para a componente horizontal da velocidade:

E essa velocidade horizontal é constante, já que a única aceleração que age sobre a bola é a gravitacional, que é totalmente vertical.