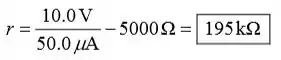Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 25.1 - Ex. 94

Você recebe um galvanômetro D'Arsonval que desviará da escala completa se uma corrente de 50,0 μ A passar pelo galvanômetro. Nesta corrente, há uma queda de tensão de 0,250 V no medidor. Você deseja usar este galvanômetro para construir um voltímetro que pode medir diferenças de potencial de até 10,0 V. Mostre que isso pode ser feito colocando uma grande resistência em série com o movimento do medidor e encontre a resistência necessária.

Passo 1

Eae galera! Tudo tranquilo? Tendo uma visão geral da coisa, o diagrama de circuito mostra um fragmento de um circuito no qual um resistor de resistência r está conectado em série com o movimento do medidor do Problema 92. O objetivo deste resistor é limitar a corrente através do movimento do galvanômetro a 50 μ A e produzir um deflexão do movimento do galvanômetro que é uma medida da diferença de potencial V.

Passo 2

Vamo lá. Aplique a regra de loop de Kirchhoff ao fragmento de circuito para obter:

Resolvendo para r resulta:

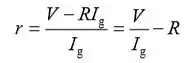
Use a lei de Ohm para relacionar a Ig atual através do movimento do galvanômetro à diferença de potencial Vg através dele:

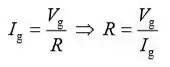
Use os valores de Vg e Ig fornecidos no Problema 114 para avaliar R:

Substituindo numericamente,

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quando os faróis de um automóvel são acesos, um amperímetro em série com os faróis indica 10,0 A e um voltímetro em paralelo com os faróis indica 12,0 V (Fig. 27-60). Quando o motor de arranque é acio

Na Fig. 27-61, o valor de R , pode ser ajustado através de um contato deslizante até que os potenciais dos pontos a e b sejam iguais . (Um teste para verificar se essa condição foi satisfeita é ligar

(a) Na Fig. 27-56, determine a leitura do amperímetro para E = 5,0 V (fonte ideal), R 1 = 2,0 Ω , R 2 = 4,0 Ω e R 3 = 6,0 Ω . (b) Mostre que se a fonte for colocada na posição do amperímetro e vice-ve

Um ohmímetro simples é construído ligando uma pilha de lanterna de 1,50 V em série com uma resistência R e um amperímetro capaz de medir correntes entre 0 e 1,00 mA, como mostra a Fig. 27-59. A resist

Se os pontos a e b na Fig. 29-44 forem ligados por um fio de resistência r, mostre que a corrente no fio será i = E R s - R x R + 2 r R s + R x + 2 R s R x onde E é a fem da bateria ideal. Suponha que