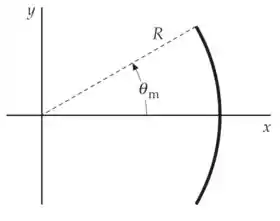
Você tem um arame uniforme e fino dobrado em um arco circular, que é descrito por um raio e um ângulo (veja a figura). Mostre que a localização do centro de massa do é sobre o eixo , a uma distância , onde é expresso é radianos. Verifique sua resposta mostrando que ela dá o limite fisicamente esperado para . Verifique que a sua resposta dá o resultado previsto pelo livro (na subseção “Encontrando o Centro de Massa por Integração”) para o caso especial em que .

E o ângulo vai variar de e :

A integral de cima dá o seguinte:

E lembrando que :

E a integral de baixo:

Então:

E por simetria podemos dizer que . (O sistema é simétrico em relação ao eixo ).

Vamos analisar o caso em que , mas lembrando de expressar em radianos:

Ou seja, nesse caso, a posição do centro de massa é . Isso faz sentido?

Bom, quando , o arame forma um círculo completo, e nesse caso é claro que o centro de massa coincide com o centro geométrico mesmo. Então a resposta faz sentido.

No caso em que , então:

Que é justamente o resultado que aparece no livro.