Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 2- Ed: 14º - Capítulo 14.Problemas - Ex. 86

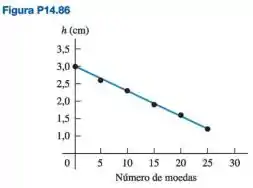
Você tem um balde contendo um líquido desconhecido. Também tem um bloco de madeira em forma de cubo com 8,0 cm de lado, mas não sabe sua massa ou sua densidade. Para descobrir a densidade do líquido, você realiza uma experiência. Primeiro, coloca o bloco no líquido e mede a altura do topo do bloco flutuante acima da superfície do líquido. Depois, empilha diversas quantidades de moedas de 25 centavos de dólar sobre o bloco e mede o novo valor de h. A linha reta que oferece o melhor ajuste aos dados que você coletou aparece na Figura P14.86. Ache a massa de uma moeda de 25 centavos (consulte em as moedas datadas de 2012). Use essa informação e a inclinação e interceptação do ajuste da linha reta aos seus dados para calcular (a) a densidade do líquido (em k g / m 3 ) e (b) a massa do bloco (em kg).

Passo 1

Oii pessoal, show de bola??

“A loucura é como a gravidade, só precisa de um empurrãozinhooo...”

Bora empurrar e macetar essa questãozinha comigo agora

Para resolver esta questão, devemos colocar em pratica os conceitos sobre densidade, empuxo e volume submerso de um corpo suspenso por um fluido.

  1. Para medir a densidade do fluido, inicialmente vamos aplicar a equação que relaciona a altura emersa com o número de moedas. Sabe-se que o peso do conjunto formado pelo bloco e moedas é igual ao empuxo sofrido pelo bloco. A altura das moedas não entrará neste cálculo, apenas a massa delas. Portanto, a equação da reta será:

    2. E = P

    ρ l i q u i d o g V d e s l o c a d o = M b l o c o + n ⋅ m m o e d a g

    ρ l i q u i d o ⋅ 0,08 2 ⋅ L = M b l o c o + n 5,67 × 10 - 3

    0,08 - h = M b l o c o + n 5,67 × 10 - 3 0.08 2 ⋅ ρ f l u i d o

    h = 0,08 - M b l o c o + n 5,67 × 10 - 3 0.08 2 ⋅ ρ f l u i d o - 5.67 × 10 - 3 0.08 2 ⋅ ρ f l u i d o n

    Passo 2

    Para calcular a densidade, basta encontrar a inclinação da reta. A inclinação é o termo que multiplica a variável da reta, ou, seja, n. A inclinação é a razão entre a variação do h e a variação do n, ou seja:

    ∆ h ∆ n = i n c l i n a ç ã o

    0,025 - 0,03 5 - 0 = - 5.67 × 10 - 3 0.08 2 ⋅ ρ f l u i d o

    ρ l i q u i d o = 885,9   k g / m 3

    Portanto, a densidade do líquido vale 885,9   k g / m 3

    Passo 3

  2. A massa do bloco será dada utilizando a interseção. Como já obteve o valor da densidade, basta agora pegar o valor do gráfico na qual o número de moedas é igual a zero. Ou seja, o termo independente. Temos:

h = 0,08 - M b l o c o + n 5,67 × 10 - 3 0.08 2 ⋅ ρ f l u i d o - 5.67 × 10 - 3 0.08 2 ⋅ ρ f l u i d o n

h 0 = 0,08 - M b l o c o 0.08 2 ⋅ ρ f l u i d o

0,03 = 0,08 - M b l o c o 0.08 2 ⋅ 885,9

M b l o c o = 0,2836   k g

Portanto, pode se concluir que a massa do bloco vale 0,2836   k g .

“Faça seus medos terem medo de você”

Resposta

(a) Portanto, a densidade do líquido vale 885,9   k g / m 3 .

(b) Portanto, pode se concluir que a massa do bloco vale 0,2836   k g .

Exercícios de Livros Relacionados

Um bloco de gelo flutua sobre um lago de água doce. Qual deve ser o volume mínimo do bloco para que uma mulher de 65,0 kg possa ficar em pé sobre o bloco sem molhar os pés?
Um cano de 950 kg flutua verticalmente na água do mar. O diâmetro do cano é igual a 0,900 m. Calcule a distância vertical adicional que o cano deverá afundar quando um homem de 80,0 kg ficar em pé sob
Quando um barco aberto possui uma massa de 5.750 kg, incluindo carga e passageiros, ele flutua com a água bem no topo de seu costado em um lago de água doce. (a) Qual é o volume desse barco? (b) O cap
Uma bola de plástico de raio igual a 12,0 cm flutua na água com 24,0% de seu volume submerso. (a) Que força você precisa aplicar à bola para mantê-la em repouso completamente abaixo da superfície da á
Um cubo de gelo (água congelada) de 0,180 kg está flutuando na glicerina. A glicerina está em um cilindro alto que possui raio interno de 3,50 cm. O nível da glicerina está bem abaixo do topo do cilin