Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 40.Exercícios - Ex. 13

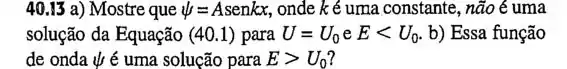
Passo 1

letra a)

A equação de Schrödinger em um dimensão é:

- ((h // 2 pi) ^2)/(2 m) (d ^2 Psi ( x ))/(d x ^2) + U ( x ) Psi ( x ) = E Psi ( x )

Precisamos substituir psi ( x ) = A s e n k x e mostrar que não é solução.

Passo 2

Substituindo:

- ((h // 2 pi) ^2)/(2 m) (d ^2 (A s e n k x))/(d x ^2) + U _o (A s e n k x) = E (A s e n k x)

- ((h // 2 pi) ^2)/(2 m) (- A k^2 s e n k x) + U _o (A s e n k x) = E (A s e n k x)

((h // 2 pi) ^2 k^2)/(2 m) (A s e n k x) + U _o (A s e n k x) = E (A s e n k x)

((h // 2 pi) ^2)/(2 m) k ^2 Psi ( x ) + U _o Psi ( x ) = E Psi ( x )

Temos então:

[((h // 2 pi) ^2)/(2 m) k ^2 + U _o] Psi ( x ) = E Psi ( x )

Com essa equação temos que:

((h // 2 pi) ^2)/(2 m) k ^2 + U _o = E

Logo a energia é maior que o potencial.

Contudo, a partir do enunciado temos que U _o > E .

Então a função dada não é solução!

Passo 3

letra b)

Se pegarmos a equação final que encontramos no item anterior:

((h // 2 pi) ^2)/(2 m) k ^2 + U _o = E

Podemos perceber que U _o < E . Pelo enunciado, é solução!

Resposta

letra b)É solução.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A Fig. 39-28a mostra o diagrama de níveis de energia de um poço de potencial unidimensional finito que contém um elétron. A região não quantizada começa em E 4 = 450,0e V . A Fig. 39-28b mostra o espe
Exercício de Livro
Exercício de Livro
Exercício de Livro