Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 40.Exercícios - Ex. 18
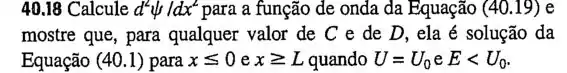
Passo 1
Precisamos mostrar que e solução da equação:
E calcular para essa função de onda.
Passo 2
Por facilidade, vamos começar com a derivada.
Passo 3
Para sabermos se é solução, basta substituirmos essa função de onda na equação:
Sabemos que , então:
Acabamos de encontrar o primeiro termo do lado esquerdo da igualdade. Substituindo ele:
Assim, a função de onda dada é solução.
Resposta
Exercícios de Livros Relacionados
Um eletrôn. no estado n = 2 do poço de potencial finito da Fig. 39-7 absorve uma energia de 400e V de uma fonte externa. Use o diagrama de níveis de energia da Fig. 39-9 para determinar a energia ciné
A Fig. 39-29a mostra um tubo fino no qual foi montado um poço de potencial finito, com V 2 = 0 . Um elétron se move para a direita no interior do poço, em uma região onde a tensão é V 1 = - 9,00V , co
A Fig. 39-9 mostra os níveis de energia de um elétron confinado em um poço de potencial finito com 450e V de profundidade. Se o elétron se encontra no estado n = 3 , qual é a sua energia cinética?
( a ) Mostre que para a região xL do poço de potencial finito da Fig. 39-7, ψ x = D e 2 k x , é uma solução da equação de Schrödinger unidimensional, onde D é uma constante e k é um número real positi
A Fig. 39-28a mostra o diagrama de níveis de energia de um poço de potencial unidimensional finito que contém um elétron. A região não quantizada começa em E 4 = 450,0e V . A Fig. 39-28b mostra o espe